Enunciado
Cálculo - Cálculo com Geometria Analítica Volume 1 - 3ª Edição - Louis Leithold- Ed: 3º - Capítulo 6.1 - Ex. 41
41. Um sólido de revolução é formado pela rotação, em torno do eixo x, da curva limitada pela curva pelo eixo x, pelo eixo y, e pela reta x=c (c>0). Para que valor de c o volume será de unidades cúbicas?
Passo 1
Antes de tudo, vamos esboçar essas curvas,
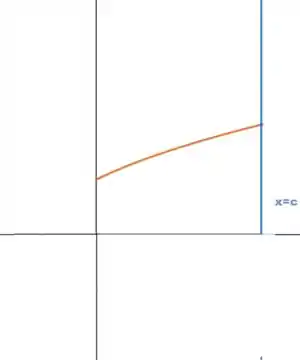
Rotacionado-as em torno do eixo x, temos
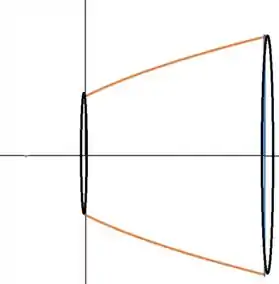
Se fizermos um corte no meio desse sólido, obteriámos uma fatia no formato de disco.
Passo 2
A aréa do disco
Passo 3
A integral ficará assim:
Lembrando que x está variando entre 0 e c.
Resolvendo a integral:
Aaaahh, mas a questão não acaba por aí, lembra que o volume tem que ser
Então, vamos lá!
Resolvendo essa equação do segundo grau obteremos dois valores para c: 2 e -6, mas c tem que ser maior que zero, portanto,
Resposta
Exercícios de Livros Relacionados
Cada integral representa o volume de um sólido. Descreva o sólido. π ∫ 0 π / 2 cos ² x . d x ²
Cada integral representa o volume de um sólido. Descreva o sólido. π ∫ 2 5 y . d y
Encontre o volume do sólido obtido pela rotação da região limitada pelas curvas dadas em torno das retas especificadas. Esboce a região, o sólido e um disco ou arruela típicos x = 2 y ,x = 0 ,y = 9 ;e
Encontre o volume do sólido obtido pela rotação da região limitada pelas curvas dadas em torno das retas especificadas. Esboce a região, o sólido e um disco ou arruela típicos y = ln x ,x = 0 ,y = 1
Encontre o volume do sólido obtido pela rotação da região limitada pelas curvas dadas em torno das retas especificadas. Esboce a região, o sólido e um disco ou arruela típicos y = x 2 ,x = y 2 ;e mt o