Enunciado
Cálculo - Cálculo Volume 1 - 7ª Edição - James Stewart- Ed: 7º - Capítulo 6.2 - Ex. 13
Encontre o volume do sólido obtido pela rotação da região limitada pelas curvas dadas em torno das retas especificadas. Esboce a região, o sólido e um disco ou arruela típicos
Passo 1
Opa, bora resolver esse problema! O enunciado nos dá as seguintes curvas
E pede pra a gente calcular o volume do sólido obtido pela rotação em torno do eixo da região delimitada pelas curvas acima! Depois disso temos que esboçar a região!
Antes de qualquer coisa a gente precisa conseguir visualizar o problema. Então vamos esboçar o gráfico das curvas dadas! Temos uma função trigonométrica:
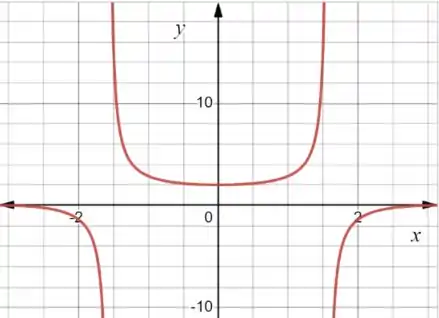
E uma reta horizontal, . Juntando as duas temos:
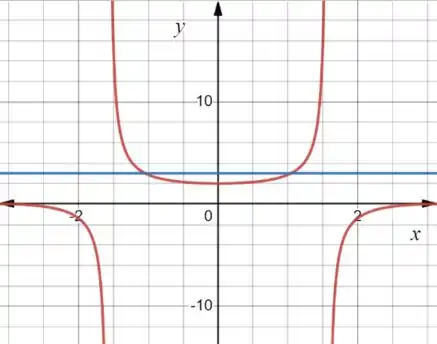
Os gráficos das funções trigonométricas tem um padrão e vão se repetindo ao longo do eixo . Aqui a gente vai trabalhar com o intervalo , beleza?!
Esses pontos onde as curvas se interceptam são:
Esses vão ser os nossos limites de integração!
Passo 2
Agora vamos a integração! Para um sólido que está entre e e possui área de seção transversal igual a , seu volume é dado por:
A área de uma coroa circular é dada por:
Onde é o raio maior e é o raio menor, que são dados em relação a . Vamos desenhar ela no gráfico pra ficar mais visível:
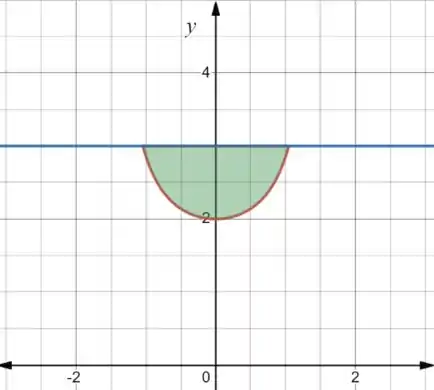
Assim, o raio maior é dado por:
E o raio menor é dado por:
Passo 3
Utilizando a definição de volume de sólido de revolução, podemos escrever a seguinte integral:
Vou trazer o gráfico pra pertinho de novo:
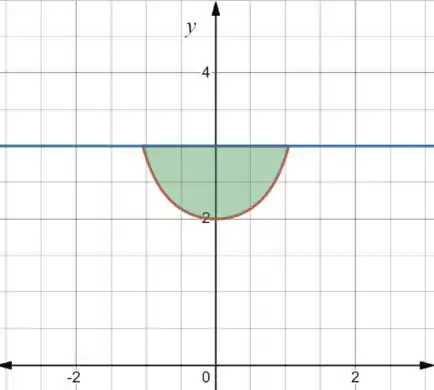
A área que a gente quer é essa verdinha. Perceba a simetria da figura! Com isso, a gente pode calcular a integral no intervalo e depois dobrar!!
Assim, resolvendo a integral, temos
Passo 4
Podemos esboçar graficamente a região e o sólido da seguinte maneira:
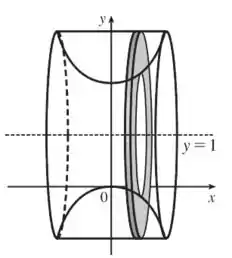
Prontinho!