Encontre o volume do sólido obtido pela rotação da região limitada pelas curvas dadas em torno das retas especificadas. Esboce a região, o sólido e um disco ou arruela típicos
Passo 1
Fala aee, tranquilo??
Bom, galera, nessa questão queremos encontrar o volume do sólido gerado ao rotacionar a função apresentada em torno do eixo . Temos aqui a seguintes cruvas:
Para isso, utilizaremos o conceito de Volume de Sólidos de revolução e as técnicas de integração para calcular o valor desse volume.
Agora vamos plotar as curvas dadas pra descobrir a região que queremos esboçar:
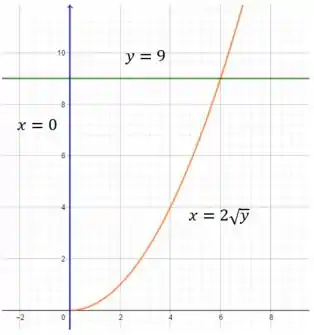
Tudo que está entre essas duas retas e o gráfico, ok? Em torno de .
Pra calcular o volume do nosso sólido vamos usar a fórmula:
Repara que nesse caso a gente vai integrar com respeito a porque a própria equação está em função de . Mas a gente também poderia fazer em função de , é só isola-lo!
Olhando o gráfico a gente já consegue tirar os limites de integração! Teremos:
Repara no gráfico que esses são os valores de que delimitam a nossa região!
Passo 2
Utilizando a definição de volume de sólido de revolução, podemos escrever a seguinte integral
Resolvendo a integral, temos
Passo 3
Podemos esboçar graficamente o sólido da seguinte maneira:
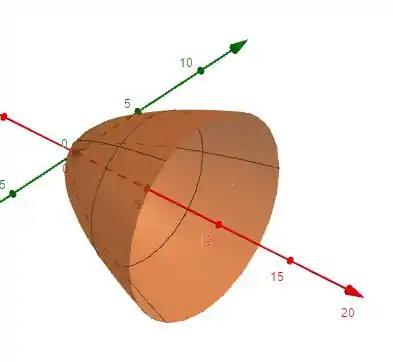
Prontinho. Só isso :)