Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo com Geometria Analítica Volume 1 - 3ª Edição - Louis Leithold- Ed: 3º - Capítulo 4.8 - Ex. 41

41. Uma viga de 27m é transportada horizontalmente por uma passagem com 8 m de largura, e então por um corredor em ângulo reto com a passagem. Qual deve ser a largura do corredor para que a viga possa passar por essa quina? Despreze a dimensão transversal da viga, ou seja, considere-a como um segmento de reta.

Passo 1

Nós precisamos achar uma função para a largura do corredor e ela deve ser a máxima para que a viga passe.

Passo 2

Vamos chamar de θ o ângulo entre a viga e o corredor, então 8 c o s s e c θ metros da viga estão na passagem e 27 - 8 c o s s e c θ metros estão no corredor central. Sendo a distância da ponta da viga até o corredor central s , precisamos do valor máximo de s .

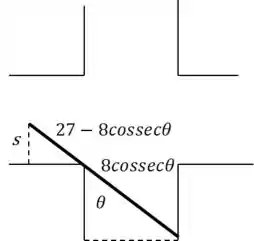
Passo 3

Queremos que essa distância s seja máxima, então vamos derivar e igualar a 0 pra achar um t que satisfaça isso.

s θ = 27 - 8 c o s s e c θ c o s θ = 27 c o s θ - 8 c o t g θ

s ' θ = - 27 s e n θ + 8 c o s s e c 2 θ = 8 - 27 s e n 3 θ s e n 2 θ

s ' θ = 0

8 - 27 s e n 3 θ = 0

8 = 27 s e n 3 θ

s e n θ = 2 3

Então cos ⁡ θ = 5 3 e c o t g θ = 5 2

Passo 4

Agora, vamos substituir esses valores de c o s ( θ ) e c o t g θ ...

s θ = 27 5 3 - 8 5 2 = 5 5

Essa é a largura do corredor

Resposta

L a r g u r a = 5 5   m e t r o s

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um retângulo será inscrito em um arco da curva y = 4 cos ⁡ 0,5 x , de x = - π a x = π . Quais as dimensões do retângulo de maior área, e qual é a maior área?
Uma folha de papelão com medidas 24 × 36p o l . É dobrada ao meio para formar um retângulo de 24 × 18p o l . , como mostra a figura a seguir. Depois, quatro quadrados congruentes com lados medindo x s
Uma janela possui a forma de um retângulo sob um semisírculo. O retângulo será de vidro transparente, enquanto o semicírculo será de vidro colorido, que transmite apenas metade da luz incidente, por u
Determine as dimensões de um cilindro circular reto com o maior volume possível que possa ser inscrito em uma esfera de raio 10c m . Qual o seu volume máximo?
a ) Suponha que, em vez de uma caixa com base quadrada, você possua uma caixa com lados quadraso cujas dimensões sejam h × h × w e cuja cintura seja 2 h + 2 w . Que dimensões darão À caixa o maior vol