Enunciado
Cálculo - Cálculo - 12ª Edição - Maurice D. Weir e Joel Hass (George B. Thomas)- Ed: 12º - Capítulo 4.6 - Ex. 18
Um retângulo será inscrito em um arco da curva , de a . Quais as dimensões do retângulo de maior área, e qual é a maior área?
Passo 1
Vamos olhar como é a figura desse retângulo nessa curva:
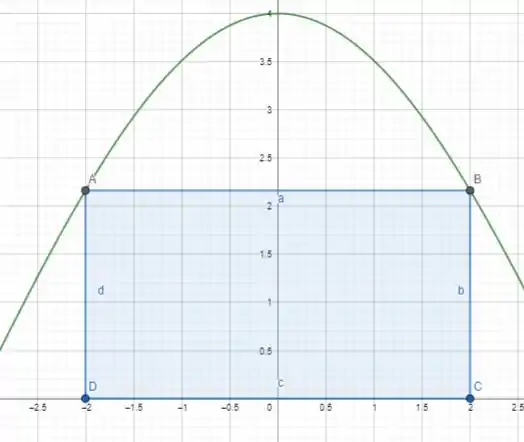
Se pegarmos as coordenadas daquele ponto sendo e
Vamos ter:
Assim, nosso retângulo tem dimensões sendo:
E a área vai ficar:
Com o indo de até , que é a limitação que ele deu.
Passo 2
Para achar a maior área possível, temos que achar o ponto de máximo de .
Para isso, temos que ver se existe algum extremo no intervalo de e comparar com os extremos do intervalo.
Vamos começar achando a derivada. Para isso, devemos usar a regra do produto:
Ela vai ser em:
Essa equação só sai se usarmos algum programa, não tem como resolver na mão.
Usando o geogebra, vamos ter o seguinte gráfico para essa função:
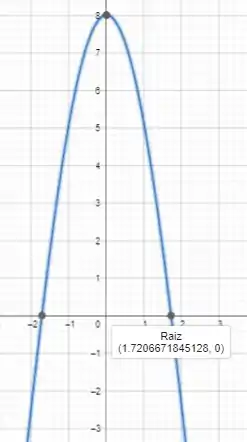
Assim, temos que:
É ponto crítico.
Passo 3
Aproveitando o gráfico, vemos que a primeira derivada muda de sinal em .
Ela vai do crescente, porque é positiva, para o decrescente. Então é ponto de máximo local.
Passo 4
Vamos comparar agora os valores de no máximo local e nos extremos do intervalo. Para isso, vamos usar uma calculadora.
Então vamos ter que a área máxima é .
Vamos achar as dimensões do retângulo.
Fazendo
Resposta
a área máxima é .