Enunciado
Cálculo - Cálculo - 12ª Edição - Maurice D. Weir e Joel Hass (George B. Thomas)- Ed: 12º - Capítulo 4.6 - Ex. 22
Uma janela possui a forma de um retângulo sob um semisírculo. O retângulo será de vidro transparente, enquanto o semicírculo será de vidro colorido, que transmite apenas metade da luz incidente, por unidade de área, em relação ao vidro transparente. O perímetro total é fixo. Determine as proporções da janela que permitirão a maior passagem de luz. Ignore a espessura do caixilho.
Passo 1
Considerando que a quantidade de luz que passa no vidro colorido é metade do transparente, podemos fazer a seguinte fórmula para a quantidade de luz que passa
Com
Assim:
O quanto passa de luz depende só da área. Então, fazendo o raio do semicírculo sendo e a altura do retângulo sendo , vamos ter:
A quantidade de luz será:
𝐸le disse que o perímetro é fixo, vamos chamar de
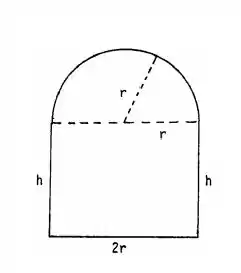
Tiramos isso da figura acima.
Isolando o
A quantidade de luz vai ficar:
O valor de pode ir de , até quando não temos altura e o comprimento da semicircuferência vale
Então:
Passo 2
Para acharmos o valor de mínimo ou máximo, temos que comparar o valor da função nos pontos críticos e nos extremos do intervalo.
Começando por achar os pontos críticos:
Fazendo isso igual a
Colocnado o em evidência do lado esquerdo:
Passo 3
Como a fórmula da nossa quantodade de luz é uma função de grau, vamos ter que aquele ponto crítico vai acabar sendo um ponto de máximo.
Suas dimensões serão
E
Vamos ter que a proporção vai ser: