Enunciado
Cálculo - Cálculo com Geometria Analítica Volume 1 - 3ª Edição - Louis Leithold- Ed: 3º - Capítulo 4.8 - Ex. 42
42. Se dois corredores em ângulo reto um com o outro têm larguras de 3 e 4,5m, qual o comprimento da maior viga que pode ser movida horizontalmente, passando por essa quina? Despreze a dimensão transversal da viga.
Passo 1
Nós precisamos achar uma função para o comprimento da viga e minimizá-la para que a viga passe.
Passo 2
Vamos chamar de o comprimento da viga que toca a quina das paredes, metros do corredor de 4,5m e metros do corredor de 3m. Com a figura fica mais fácil...
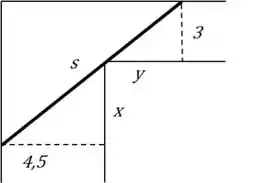
Por semelhança de triângulos, . Escrevendo como soma das hipotenusas dos triângulos menores:
Passo 3
Queremos que o comprimento seja mínimo, então vamos derivar e igualar a 0 pra achar um que satisfaça isso.
Passo 4
Agora, substituindo esse valor de em , teremos o comprimento.
Resposta
Exercícios de Livros Relacionados
Use diferenciais para aproximar o volume de material necessário para fazer uma bola de borracha se o raio da câmara interna é 2cm e a espessura da borracha é 1 8 cm.
A medida de uma raio de um cone circular reto é 4 3 vezes a medida da altura. Qual a exatidão com que a aultura deverá ser medida se o erro no volume calculado não puder exceder 3 por cento?
Se t s for o tempo para que um pêndulo complete sua volta, tendo l cm de comprimento, então 4 π 2 l = g t 2 , onde g = 32,2. Qual será o efeito sobre o tempo, se for cometido um erro de 0.01 cm na med
Um pedaço de fio com 80 cm de comprimento deve ser dobrado para formar um retângulo. Ache as dimensões do retângulo com maior área possível.
Se y = 80 x - 16 x 2 , ache a diferença Δ y - d y se (a) x = 2 e Δ x = 0,1 ; (b) x = 4 e Δ x = - 0,2 .