Enunciado
Cálculo - Cálculo Volume 1 - 7ª Edição - James Stewart- Ed: 7º - Capítulo 2.6 - Ex. 43
Encontre as assíntotas horizontais e verticais de cada curva. Confira seu trabalho por meio de um gráfico da curva e das estimativas das assíntotas.
Passo 1
Faaaala! Bora dar uma olhadinha nessa questão!
Precisamos calcular as assíntotas horizontais e verticais dessa curva aqui:
Mas como fazemos isso?
Pra encontrar as assíntotas horizontais, precisamos calcular o limite da nossa função em e em . Se encontrarmos um valor finito, então tem uma assíntota horizontal ali! Ou seja:
Se , então é uma assíntota horizontal!
E as assíntotas verticais? Esse tipo de assíntota só pode existir em pontos onde a nossa função não está definida. Então precisamos encontrar esses pontos e verificar o limite da nossa função neles. Se esse limite explodir pra ou , então temos uma assíntota vertical ali! Então:
Se , então é uma assíntota vertical.
Legal! Vamos atacar um de cada vez!
Passo 2
Vamos começar com as assíntotas horizontais. Então precisamos calcular os limites em e em . Vamos lá!
Como temos uma divisão de polinômios e , podemos usar aquela brincadeira de desprezar os termos de menor grau. Logo,
Isto é,
Então isso nos diz que temos uma assíntota horizontal em .
Se repetirmos o cálculo para , encontramos o mesmo resultado. Portanto, é a nossa única assíntota horizontal!
Passo 3
Agora vamos analisar as assíntotas verticais. Pra isso, precisamos investigar se tem algum ponto em que a nossa função não está definida. Vamos dar uma olhada:
Nossa curva não vai estar definida quando o denominador é zero, isto é:
Resolvendo a equação do segundo grau, temos:
Então,
ou
Agora vamos checar os limites da nossa função nesses pontos. Vamos começar com :
Se aplicarmos o limite, percebemos que o numerador tende a , enquanto o denominador tende a , o que significa que esse limite explode pro infinito. Se a questão estiver pedindo pra calcularmos o limite exatamente, precisamos separar nos limites laterais pra estudar os sinais do infinito. Mas nesse caso, como só queremos saber onde estão as assíntotas, essa análise já é suficiente pra dizermos que é uma assíntota vertical.
Agora vamos checar :
Aplicando o limite, descobrimos que o numerador tende a e o denominador tende a . Novamente, o limite explode pro infinito e isso é suficiente pra podermos afirmar que é uma assíntota vertical.
Portanto, temos duas assíntotas verticais:
e
Passo 4
Conferindo em um gráfico, temos:
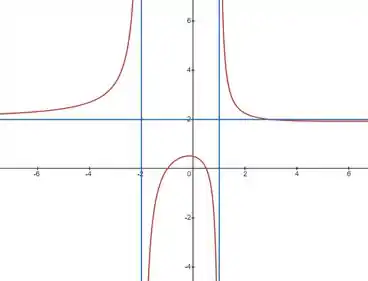
Pelo gráfico, podemos confirmar que as assíntotas estão compatíveis com o que encontramos.
Resposta
Assíntota horizontal:
Assíntotas verticais:
e