Enunciado
Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 2.6 - Ex. 6
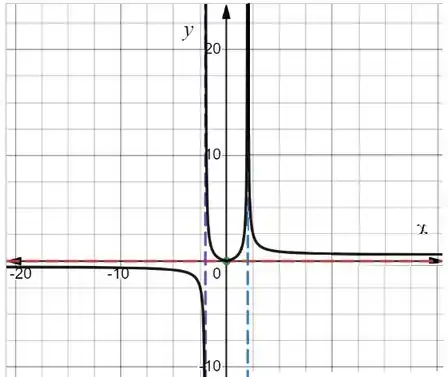
Esboce o gráfico de um exemplo de uma função que satisfaça a todas as condições dadas
Passo 1
Falaeee, belezinha? Bom.. a questão nos dá as seguintes condições abaixo e nos pede para esboçar um gráfico a partir delas:
Então vamos com muuuuita calma, entender cada informação dessas!
Mas antes vou te relembrar de alguns conceitos. Limites laterais são limites quando nos aproximamos da função por apenas um lado. E usamos esses sinaizinhos de + e – do ladinho do valor que tende. Indicando se estamos nos aproximando pela esquerda ou pela direita:
- significa que estamos nos aproximando pela esquerda e
- significa que estamos nos aproximando pela direita e
Em casos como esse, que os limites laterais são diferentes, o limite geral não existe. Pro limite de uma função num ponto existir, precisamos que os limites laterais naquele ponto existam e sejam iguais entre si. Sendo assim:
- significa que os limites laterais existem e são iguais. Se nos aproximamos de 2, seja pela direita ou pela esquerda, a função explode pro infinito positivo.
- quer dizer que quando assume valores muito muito pequenos, a função se aproxima cada vez mais de zero
- quer dizer que quando assume valores muito muito grandes, a função se aproxima cada vez mais de zero
Também sabemos o comportamento pra valores muito muito grandes ou muito muito pequenos:
Bom e sabemos também que a função passa pela origem:
Antes de começar, vou apresentar mais um último conceito: o de assíntotas horizontais e verticais. Uma assíntota é uma linha que uma curva se aproxima à medida que você segue indefinidamente ao longo da curva.
Se a função explode pro infinito quando então temos uma assíntota VERTICAL em .
Quando fazemos o limite da função pra indo pro infinito, se achamos um número finito , então temos uma assíntota horizontal em .
Chega, vamos praticar!
Passo 2
Repare que nesse tipo de questão nós temos diversas soluções. Vou fazer uma, olha só:
Se a função explode pro infinito quando então temos uma assíntota VERTICAL em .
Vamos ter duas assíntotas verticais:
e
Em a função cresce infinitamente quando nos aproximamos de pelos 2 lados.
Em , a função cresce quando nos aproximamos pela direita e decresce infinitamente, quando nos aproximamos pela esquerda.
Passo 3
Quando fazemos o limite da função pra indo pro infinito, se achamos um número finito , então temos uma assíntota horizontal em .
Quando vai pro infinito positivo, também tendemos a zero:
O limite é igual a um número finito, então temos uma assíntota HORIZONTAL em:
Passo 4
E, por fim,
nossa função passa na origem
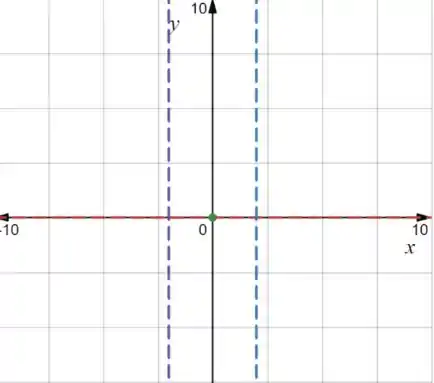
Desenhando as assíntotas. São essas 3 linhas tracejadas, vermelha, azul e roxa:
Passo 5
Vamos pensar no gráfico como se a gente tivesse trilhando um caminho, a gente vem de , passa por pela esquerda, depois pela direita, passamos por e finalmente vamos para .
Lembrando que:
Quando eu saio de eu me aproximo de e quando eu vou chegando em eu vou para .
Quando atravessamos estamos lá no infinito, mas agora positivo, lembrando que os limites laterais em -2 são diferentes. A a medida que nos aproximamos de saimos do infinito, passamos por e voltamos pro infinito!
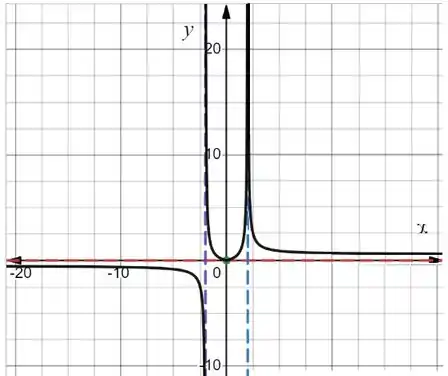
Agora a gente atravessa e nesse momento estamos no , a medida que assumimos valores maiores de nos aproximamos de .
Deu pra entender direitinho? Pronto! Conseguimos nosso gráfico!
Resposta
