Encontre o limite ou demonstre que ele não existe:
Passo 1
Fala aí, belezinha com você?
Bom galera, essa questão pede pra gente encontrar o seguinte limite:
Ou provar aqui ele não existe.
Cara, a ideia que é usar as propriedades dos limites analizando com cuidado a função para saber o que acontecerá com ela quando o tender ao .
Vem comigo que faremos exatamente isso no passo a passo.
Passo 2
A primeira propriedade que iremos usar é a de passar o limite para o argumento da função .
Assim, nosso limite se torna:
Boa. Agora vamos ver o que aconteceu lá dentro.
Passo 3
Repara que dentro do argumento ficamos com:
E esse limite podemos calcular. Basta pensar para que valor o vai quando o expoente tende ao . E termos como resposta:
Show, agora vamos voltar para a questão original.
Passo 4
Beleza, então se a gente pode escrever o limite como:
Pronto, se a gente lembrar do gráfico da função do a gente percebe que quanto maior o a função vai se aproximando de . Olha só:
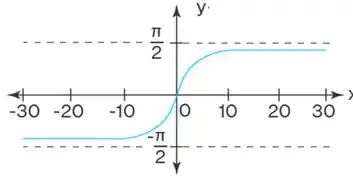
Então, vamos ter:
E prontinho. Temos a nossa resposta!