Enunciado
Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 3.10 - Ex. 43
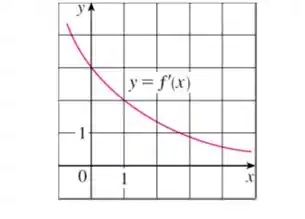
43) Suponha que a única informação que temos sobre uma função é que e que o gráfico de sua derivada é como mostrado.
(a) Use uma aproximação linear para estimar e .
(b) Suas estimativas na parte (a) são muito grandes ou pequenas? Explique.
Passo 1
Oiieeeee, vamos resolver mais uma?
Nesse problema foi dado o gráfico da derivada de uma função:
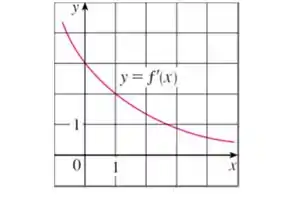
E foi dito que .
A partir daí queremos usar uma aproximação linear para determinar e .
Tem ideia de como fazemos isso?
Se o problema está falando de aproximação linear, podemos imaginar que vamos ter que aplicar a fórmula da aproximação.
Queremos a aproximação de e , que são próximos de .
Como foi dado o valor de , podemos aplicar essa fórmula de para e pode ser obtida pelo gráfico de .
Sacou? Bora começar!
Passo 2
Pelo gráfico de , temos:
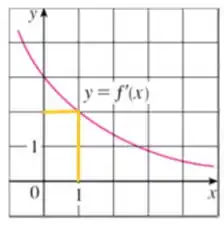
Assim, como , aplicando essas informações na função linearização:
Show? Agora para , temos:
Agora para :
Pelo gráfico, vemos a derivada da função é positiva e decrescente, isso implica que a função é crescente e possui a concavidade é votada para baixo. Ou seja, a função tem um crescimento menor e as retas tangentes estão acima da função , logo, as estimativas são muito grandes em relação a .
E aí! o que achou? Responde Aí!
Resposta
(a) e
(b) As estimativas são muito grandes em relação a .