Encontre as assíntotas horizontais e verticais de cada curva. Confira seu trabalho por meio de um gráfico da curva e das estimativas das assíntotas.

Começando pelas assíntotas horizontais, vamos analisar os limites para e .

Nesse caso vamos aplicar um método de solução que consiste em dividir o numerador e o denominador pelo termo de maior grau do denominador.

Nesse caso, o termo de maior grau no denominador é , ou seja

Simplificando...

Perceba que quando fazemos tendendo a , os termos e tenderão a já que estamos dividindo um número muito pequeno por um número extremamente grande...

Dessa forma, chegamos no seguinte resultado do limite

Da mesma forma teremos:

Portanto, é uma assíntota horizontal.

Show de bola?

Agora vamos analisar as assíntotas verticais, isto é, quando nossa curva vai pro infinito! Lá em cima falamos que assíntotas verticais estão relacionadas a um ponto onde a nossa função não está definida, vamos observar a nossa função:

Sabemos que quando o denominador é zero, isto é:

Colocando o em evidência, temos:

Então:

Para a equação :

Dessa forma, temos três assíntotas verticais:

Tranquilo até aqui?

Fazendo o gráfico com o auxilio de uma ferramenta gráfica, temos que

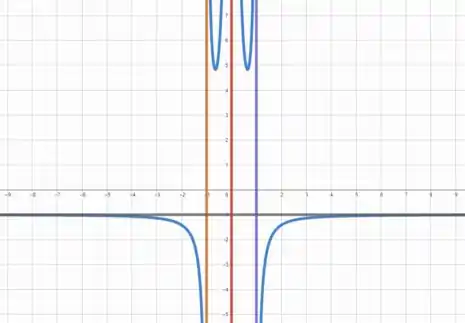
Pelo gráfico, podemos confirmar que as assíntotas são realmente aquelas.

E aí! o que achou? Responde Aí!