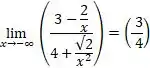Enunciado
Cálculo - Cálculo - 12ª Edição - Maurice D. Weir e Joel Hass (George B. Thomas)- Ed: 12º - Capítulo 2.6 - Ex. 8b
Determine o limite de cada função a) quando QUOTE _x0001_
Passo 1
Temos que calcular um limite no infinito, certo?
Assim como no item a), temos que se ligar que assim como nos outros cálculos de limites, podemos usar aquelas regras: do produto, da soma, do quociente e etc...
No nosso caso, como temos uma divisão, vamos usar primeiro a regra do quociente, então
Passo 2
Olhando para o denominador e o numerador da função do quociente do passo anterior, temos uma soma e uma subtração, respectivamente, então vamos usar as regra da soma (o limite da soma é a soma dos limites) e da subtração (só trocar soma por subtração na regra),
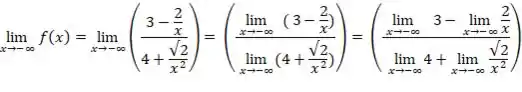
Passo 3
Agora é só substituir os resultados, mas antes temos que perceber umas coisinhas:
1ª coisa: Como 3 não depende de QUOTE _x0001_
ele é uma constante e aí pela regra da constante,
QUOTE _x0001_
Da mesma forma,
QUOTE _x0001_
2ª coisa:
QUOTE _x0001_
pela mesma justificativa do item a).
3ª Coisa:
E, como o limite do produto é o produto dos limites,
pela coisa 2.
Passo 4
Então agora é só substituir os valores:
QUOTE _x0001_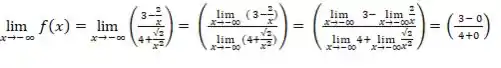
Resposta
