Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo - 12ª Edição - Maurice D. Weir e Joel Hass (George B. Thomas)- Ed: 12º - Capítulo 4.6 - Ex. 46b

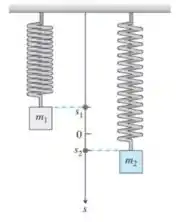
46. Duas massas penduradas por molas lado a lado possuem posições s 1 = 2 s e n   t e s 2 = s e n   2 t , respectivamente.

b. Quando, no intervalo 0 ≤ t ≤ 2 π , a distância vertical entre as massas é máxima? Qual é essa distância? (Dica: cos ⁡ 2 t = 2 c o s 2 t - 1 .)

Passo 1

b) Para descobrirmos a distância vertical máxima entre as massas, assim como o tempo em que isso ocorre, devemos fazer o seguinte, galera:

s t = s 1 - s 2

Substituindo as equações, teremos:

s t = | 2 s e n   t - s e n   2 t |

s t = 2 s e n   t - s e n   2 t 2 1 2

No entanto, o que queremos descobrir é para quando isso é máximo, certo? Para fazermos isso, temos que utilizar o conceito de máximos e mínimos: derivando a função em questão e igualando a zero, olha só:

s ' t = 1 2 . 2 s e n   t - s e n   2 t 2 - 1 2 . 2 . 2 s e n   t - s e n   2 t . 2 cos ⁡ t - 2 cos ⁡ 2 t

s ' t = 2 s e n   t - s e n   2 t . 2 cos ⁡ t - 2 cos ⁡ 2 t 2 s e n   t - s e n   2 t

Utilizando a dica dada pela questão, teremos:

s ' t = 4 . 2 cos ⁡ t + 1 cos ⁡ t - 1 . s e n   t . ( cos ⁡ t - 1 ) | 2 s e n   t - s e n   2 t |

Passo 2

Agora que derivamos nossa equação, se igualarmos a mesma a zero, teremos:

4 . 2 cos ⁡ t + 1 cos ⁡ t - 1 . s e n   t . ( cos ⁡ t - 1 ) | 2 s e n   t - s e n   2 t | = 0

4 . 2 cos ⁡ t + 1 cos ⁡ t - 1 . s e n   t . cos ⁡ t - 1 = 0

Para que esse produto imenso resulte em zero, os resultados de t são:

t = 0 ; 2 π 3 ;   π ; 4 π 3   e   2 π   s e g u n d o s

Substituindo cada ponto na expressão inicial da distância, teremos:

s 0 = 2 s e n   0 - s e n   2 . 0 = 0  

s 2 π 3 = 2 s e n   2 π 3 - s e n   2 . 2 π 3 = 3 3 2

s π = 2 s e n   π - s e n   2 . π = 0

s 4 π 3 = 2 s e n   4 π 3 - s e n   2 . 4 π 3 = 3 3 2

s 2 π = 2 s e n   2 π - s e n   2.2 π = 0

Com os resultados, podemos concluir que o maior valor da distância vertical entre as massas é 3 3 2 , que ocorre nos intervalos t = 2 π 3   e   4 π 3   .

Resposta

b) Distância máxima: 3 3 2

Tempo em que ocorre: t = 2 π 3   e   4 π 3

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Encontrar o tamanho máximo que a escada pode ter.
As posições de duas partículas no eixo s são s 1 = c o s t e s 2 = cos ⁡ t + π 4 . Quando as partículas colidirão ?
Caixa sem tampa Uma caixa retangular, sem tampa, será confeccionada a partir de uma folha de papelão de 10 x 16 pol., recortando-se os vértices quadrados com lados iguais e dobrando-se os lados para c
9- Os lados x e y de um retângulo estão variando a taxas constantes de 0,2 m/s e 0,1 m/s, respectivamente. A que taxa estará variando a área do retângulo no instante em que x = 1m e y = 2m ?
10-A altura h e o raio r de um cone circular reto estão variando a taxas constantes de 0,1m/s e 0,3m/s, respectivamente. A que taxa estará variando o volume do cone no instante em que h=0,5m e r=0,2m?