Enunciado
Cálculo - Cálculo - 12ª Edição - Maurice D. Weir e Joel Hass (George B. Thomas)- Ed: 12º - Capítulo 4.6 - Ex. 44
44. Rigidez de uma viga. A rigidez S de uma viga retangular é proporcional à sua largura multiplicada pelo cubo de sua profundidade.
a. Determine as dimensões que produzem a viga mais rígida que poderá ser cortada a partir de um tronco de 12 pol. de diâmetro.
b. Esboce o gráfico de em função da largura da viga, considerando que a constante de proporcionalidade seja. Concilie o que observou neste item com a sua resposta no item (a).
c. Na mesma tela, esboce o gráfico de em função da profundidade do sarrafo, mantendo . Compare um gráfico com o outro e com a sua resposta do item (a). Qual seria o efeito de mudar para algum outro valor de ? Experimente.
Passo 1
a) Segundo o enunciado, a rigidez de uma viga é proporcional à sua largura multiplicada pelo cubo de sua profundidade. Se escrevermos uma expressão para isso, teremos:
Mas quem é esse ? Como o enunciado fala sobre proporcionalidade, então é a constante de proporcionalidade da equação, ok? Mas quem é ? Se utilizarmos o teorema de Pitágoras, teremos:
Substituindo na equação da rigidez, teremos:
Passo 2
Agora que temos uma expressão para a rigidez, como fazemos para descobrir o valor máximo da mesma? Basta utilizarmos o conceito de máximo e mínimo, galera! Derivando a função em questão e igualando a zero, teremos:
Sim, devemos utilizar a regra do produto, no qual:
Substituindo na regra do produto, teremos:
Igualando a zero, temos:
Sendo assim, o ponto crítico que nos interessa será . Para esse valor de , valerá:
Dessa forma, as dimensões que produzem a viga mais rígida são:
Passo 3
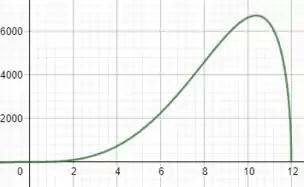
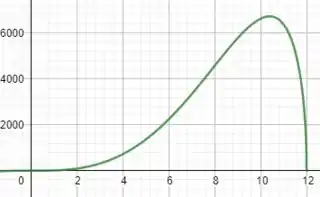
b) Se plotarmos o gráfico de , teremos:
Passo 4
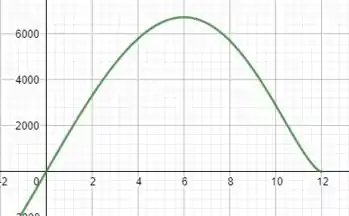
c) Se plotarmos o gráfico de , teremos:
Já respondendo à letra b) também, temos que os dois gráficos indicam o mesmo valor máximo para a rigidez da viga, o que faz sentido. Ademais, alterar não surte efeito algum!
Resposta
a)
b)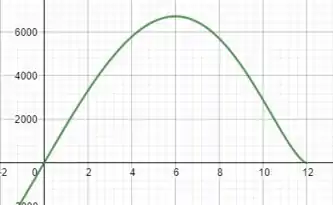 
c) 