Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo - 12ª Edição - Maurice D. Weir e Joel Hass (George B. Thomas)- Ed: 12º - Capítulo 4.Exercícios Práticos - Ex. 93

Caixa sem tampa Uma caixa retangular, sem tampa, será confeccionada a partir de uma folha de papelão de 10 x 16 pol., recortando-se os vértices quadrados com lados iguais e dobrando-se os lados para cima. Determine analiticamente as dimensões da caixa de maior volume e seu volume máximo. Fundamente sua resposta graficamente.

Passo 1

Podemos representar graficamente o problema da seguinte forma:

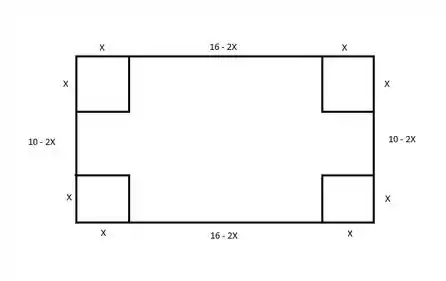
Logo, ao dobrar os lados pra cima, teremos uma caixa sem tampa com dimensões 10 - 2 x , 16 - 2 x , x . Portanto, o volume da caixa é dado pela expressão:

V = x . 10 - 2 x . ( 16 - 2 x )

Passo 2

A fim de maximizar o volume da caixa, devemos derivar e igualar a zero:

V = x 10 - 2 x . 16 - 2 x = 160 x - 20 x 2 - 32 x 2 + 4 x 3 = 4 x 3 - 52 x 2 + 160 x

V ' = 12 x 2 - 104 x + 160 = 0

3 x 2 - 26 x + 40 = 0

x 1 = 26 + 26 2 - 3.4 . 40 6 = 26 + 14 6 = 20 3

x 2 = 26 - 26 2 - 3.4 . 40 6 = 26 - 14 6 = 2

Vemos que para x 1 = 20 3 , teríamos 10 - 2 x = 10 - 2.20 3 = - 10 3 (não convém)

Portanto, podemos garantir que x = 2 .

Passo 3

Assim, as dimensões da caixa são:

x = 2

10 - 2 x = 6

16 - 2 x = 12

Resposta

As dimensões da caixa de maior volume são:

Base: 6   p o l .     p o r     12 p o l .

Altura: 2   p o l .

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Ache uma equação da reta tangente à curva y = x 3 - 3 x 2 + 5 x com inclinação mínima.
Sejam f ( x ) e g ( x ) as funções deriváveis traçadas aqui. O ponto c é onde a distância vertical entre as curvas é máxima. Há algo especial sobre as tangentes às duas curvas em c ? Justifique sua re
Você foi incumbido de determinar se a função f ( x )=3+4c o sx+c o s2 x é negativa em algum momento. A. Explique por que você precisa considerar apenas os valores de x do intervalo [ 0 ,2 π ] .B. f é
Qual é a distância mínima da curva y= x ao ponto ( 3 2 ,0 ) ? (Dica: minimizando o quadrado da distância, você evita trabalhar com raízes quadradas.)Trace o gráfico da função distância D(x) juntamente
a. A função y=c o t gx- 2c o s s e cx possui um valor máximo absoluto no intervalo 0xπ . Determine-o.b. Esboce o gráfico da função e compare o que você observa com a resposta do item (a).