Enunciado
Cálculo - Cálculo - 12ª Edição - Maurice D. Weir e Joel Hass (George B. Thomas)- Ed: 12º - Capítulo 4.6 - Ex. 46a
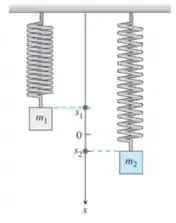
46. Duas massas penduradas por molas lado a lado possuem posições e , respectivamente.
a. Em que instante do intervalo elas passam uma pela outra? (dica: .)
Passo 1
a) Então galera, as molas passam uma pela outra quando suas posições em são iguais, não é mesmo? Dessa forma, para descobrirmos o instante de tempo em que isso ocorre, basta igualarmos as duas funções, se liga:
Utilizando a dica que nos diz que , teremos:
Os valores de para que isso ocorra, se pensarmos no ciclo trigonométrico, são em todos os pontos que são múltiplos de , certo? Dessa forma, os instantes serão:
Claro, adotando apenas valores positivos de !
Resposta
Exercícios de Livros Relacionados
13- O raio r e a altura h de um cilindro circular reto estão variando de modo a manter constante o volume V . Num determinado instante h = 3 c m e r = 1 c m e, nesse instante, a altura está variando a
12-Num determinado instante, as arestas de um paralelepípedo medem a , b , c( m ) e, neste instante, estão variando com velocidades v a , v b , v c (m/s), respectivamente. Mostre que nesse instante o
O volume V e o raio r da base de um cone circular reto estão variando com taxas constantes de 0,1 πm 3 / s e 0,2 m / s , respectivamente. Expresse d h d t em termos der e V , em que h é a altura do co
14-Uma piscina tem 10m de largura, 20m de comprimento, 1m de profundidade nas extremidades e 3m no meio, de modo que o fundo seja formado por dois planos inclinados. Despeja-se água na piscina a uma t
15-Num determinado instante θ = π 3 e está variando, nesse instante, a uma taxa de 0,01 radianos por segundo (veja figura). A que taxa estará variando o ângulo α nesse instante? 5m θ α 2m