Enunciado
Cálculo - Anton - Cálculo - Vol 1- Ed: 10º - Capítulo 1.3 - Ex. 45
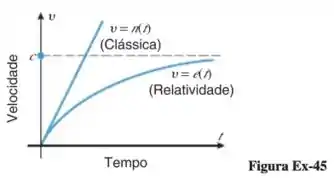
Suponha que uma partícula esteja sendo acelerada por uma força constante. As duas curvas e da figura abaixo fornecem as curvas da velocidade instantânea versus tempo para a partícula conforme previstas, respectivamente, pela Física Clássica e pela Teoria da Relatividade Especial. O parâmetro representa a velocidade da luz. Usando a linguagem de limites, descreva as diferenças nas previsões em longo prazo das duas teorias.
Passo 1
Então pessoal, o que o enunciado quer que façamos é uma análise das duas curvas para quando é infinitamente grande. Se observarmos a curva facilmente conseguimos notar que a curva cresce indefinidamente para um muito grande, ou seja:
Para a Física Clássica não há uma velocidade limite, isto é, a velocidade de um objeto poderia alcançar velocidades gigantescas caso conseguíssemos desenvolver um aparato para realizar tal aceleração. Essa é a análise para a primeira curva, agora vamos ver a segunda!
Passo 2
Se observarmos com cuidado a segunda curva, ou seja, a função , sem muita dificuldade conseguimos notar que, diferentemente da curva , esta curva apresenta um limite (uma assíntota horizontal) em . Para um muito grande temos:
Para a Relatividade há uma velocidade limite, ou seja, é impossível que um corpo acelere de tal forma a ultrapassar a velocidade da luz . Em um certo momento o corpo atingirá uma velocidade limite na qual não poderá ultrapassar!
E essa é a análise das duas curvas dadas, pessoal! 😉