Defina funções , e que satisfaçam:
- não é contínua em pontos de seu domínio;
- é contínua em todos os pontos de seu domínio mas não é contínua em ;
- é contínua em todos os pontos do domínio de ;
Faça o gráfico das funções , , e .
Passo 1
- Vamos definir a função:
- Temos que :
- E temos que :
Ela não é contínua em e pois não é definida nesses dois pontos, ou seja, o denominador zera.
Passo 2
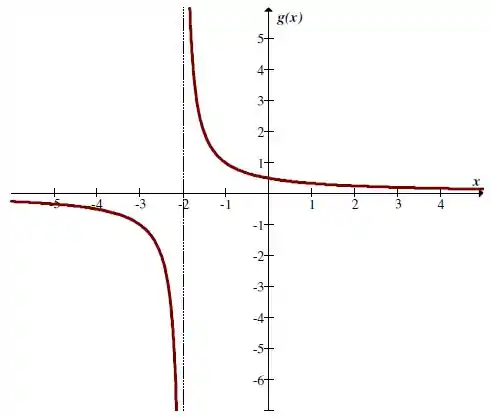
Que é contínua em todos os pontos de seu domínio, que é , mas não é contínua em .
Passo 3
aqui temos que , resultando na própria .
Passo 2
Vamos fazer os gráficos das funções:
Para temos que é definida em e é contínua em :
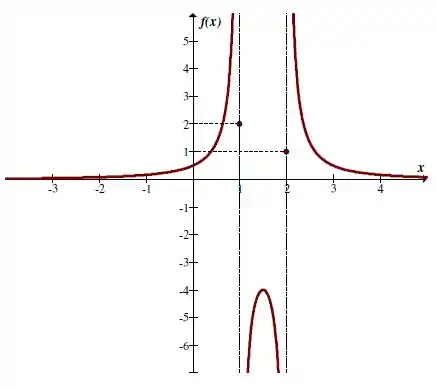
Para temos que ela é contínua em todos os pontos de seu domínio, mas não é contínua em , e o ponto não pertence ao domínio da função:
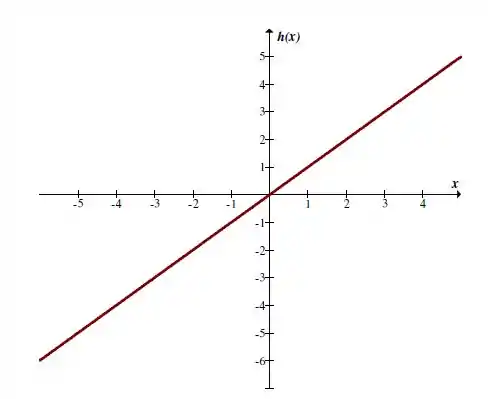
E para e temos a mesma função , que é contínua em todos os pontos do domínio: