Enunciado
Cálculo - Cálculo - 12ª Edição - Maurice D. Weir e Joel Hass (George B. Thomas)- Ed: 12º - Capítulo 4.6 - Ex. 47
47. Distância entre dois navios. Ao meio-dia, o navio estava a milhas náuticas ao norte do navio . O navio navegava para o sul a nós (milhas náuticas por hora; uma milha náutica equivale a jardas) e continuou nesse sentido durante todo o dia. O navio navegava para leste a nós e continuou nesse sentido durante todo o dia.
a. Comece com ao meio-dia e expresse a distância entre os navios em função de .
b. Qual a velocidade de mudança da distância entre os navios ao meio-dia? E uma hora mais tarde?
c. A visibilidade desse dia era de de milhas náuticas. Será que os navios podiam avistar um ao outro?
d. Esboce e em um único gráfico como funções de para , usando cores diferentes, se possível. Compare os gráficos e relacione o que você vê com suas respostas nos itens (b) e (c).
e. Parece que o gráfico de poderia apresentar uma assíntota horizontal no primeiro quadrante. Isso, por sua vez, sugere que se aproxima de um valor limite, quando . Qual é esse valor? Qual a sua relação com a velocidade individual dos navios?
Passo 1
a) Então galera, se escrevermos uma expressão de espaço para cada um dos navios, teremos o seguinte:
Note que o sinal de negativo aparece porque ele está viajando para o Sul (eixo negativo de ).
Utilizando o teorema de Pitágoras, teremos:
Passo 2
b) Para descobrirmos a velocidade de mudança de distância entre os navios, basta pegarmos a equação que achamos no passo 1 e deriva-la, uma vez que a derivada do espaço nos fornece a velocidade! Sendo assim, teremos:
Aqui vale ressaltar que a regra utilizada para a derivação foi a regra da cadeia, tudo bem? Continuando, teremos:
Para meio dia, isto é, , temos:
Para uma hora depois, temos:
Passo 3
c) Se plotarmos o gráfico de , teremos o seguinte:
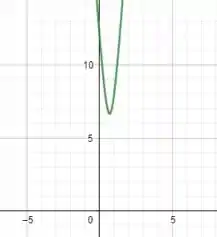
Note que o gráfico não toca em , o que nos leva a concluir que eles não se veriam!
Passo 4
d) Se plotarmos os gráficos de e , teremos o seguinte:
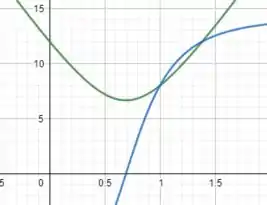
No qual a função em verde é e a função em azul é .
Passo 5
e) Aplicando o limite de na equação de , teremos:
Para facilitar nossa vida, vamos escrever essa raíz em todos os termos da razão, se liga:
Se dividirmos todos os termos dentro da raíz por , teremos o seguinte:
Aplicando o limite, teremos:
A relação desse resultado com as velocidades individuais dos navios é que esse resultado é igual à raiz quadrada da soma dos quadrados das velocidades individuais!
Resposta
a)
b)
c) Eles não se veriam!
d)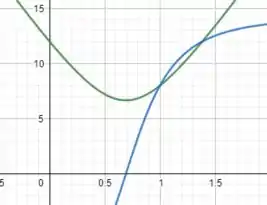 
e)