Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo com Geometria Analítica Volume 1 - 3ª Edição - Louis Leithold- Ed: 3º - Capítulo 3.8 - Ex. 47

47. Às 8 da manhã, um navio que viaja para o norte com uma velocidade de 24 nós (milhas náuticas por hora) está em um ponto P. Às 10h, um segundo navio que viaja para o leste com uma velocidade de 32 nós está em P. Qual a taxa de variação da distância entre os dois navios às (a) 9h e (b) 11h?

Passo 1

Este problema, trata-se de um problema clássico de taxas relacionadas. Para resolver este tipo de questão, primeiro devemos encontrar a função que nos fornece a taxa de variação da distância entre os dois navios. Após encontrar a mesma, basta substituir o tempo dado.

Passo 2

Para encontrar a função que nos fornece a taxa de variação , podemos utilizar o seguinte diagrama

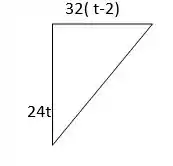
Utilizando pitágoras no diagrama acima vem que

s ( t ) 2 = 24 t 2 + [ 32 t - 2 ] 2

s = 24 t 2 + 32 t - 2 2

Passo 3

Assim, encontrada a função que modela o que está sendo pedindo no problema, devemos encontrar sua derivada, utilizando do conceito de derivação implícita . Logo, sua derivada é dada por

2 s d s d t = 2.24 t . d t d t . 24 d t d t + 2 . 32 t - 2 . d t d t . 32.1 d t d t

d s d t = 24 2 t + 32 2 ( t - 2 ) s

Passo 4

Letra (a)

A taxa de variação da distância as 9h, será

s 9 = 24.9 2 + 32 . 9 - 2 2 = 311,2

Sendo assim

d s d t = 24 2 9 + 32 2 9 - 2 311,2 = 39,7

As 9h a distância entre os navios cresce de 39,7 milhas náuticas/h

Passo 5

Letra (b)

A taxa de variação da distância as 11h, será

s 11 = 24.11 2 + 32 . 11 - 2 2 = 390,7

Sendo assim

d s d t = 24 2 11 + 32 2 11 - 2 390,7 = 39,8

As 11h a distância entre os navios aumenta de 39,8 milhas náuticas/h

Resposta

Letra (a)

As 9h a distância entre os navios cresce de 39,7 milhas náuticas/h

Letra (b)

As 11h a distância entre os navios aumenta de 39,8 milhas náuticas/h

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Uma partícula move-se ao longo da curva y = 2s e n( π x / 2 ) . Quando a partícula passa pelo ponto ( 1 3 , 1 ) , sua coordenada x cresce a uma taxa de 10c m / s . Quão rápido a distância da partícula
Suponha y = 2 x + 1 , onde x e y são funções de t. (a) Se d x / d t = 3 , encontre d y / d t quando x = 4 . (b) Se d y / d t = 5 , encontre d x / d t quando x = 12 .
Uma torneira está preenchendo uma pia hemisférica de 60c m de diâmetro com água a uma taxa de 2 L m i n . Encontre a taxa na qual a água está aumentando na pia quando estiver cheia até a metade. [Use
Se x 2 + y 2 + z 2 = 9 , d x / d t = 5 e d y / d t = 4 , encontre d z / d t quando x , y , z = ( 2,2 , 1 ) .
Uma esteira transportadora está descarregando cascalho a uma taxa de 30p é s 3 / m i n é , construindo uma pilha na forma de cone com o diâmetro da base e altura sempre igual. Quão rápido está crescen