Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo com Geometria Analítica Volume 1 - 3ª Edição - Louis Leithold- Ed: 3º - Capítulo 6.1 - Ex. 49

49. Uma cunha é cortada e um sólido com a forma e um cilindro circular reto, o qual tem um raio de r cm, por um plano através de um diâmetro da base e inclinado em relação ao plano da base segundo um ângulo cuja medida é 45°. Ache o volume da cunha.

Passo 1

Não entendeu nadinha? Senta aí que você vai ver que não é tão difícil assim.

Ilustrando o que a questão pediu:

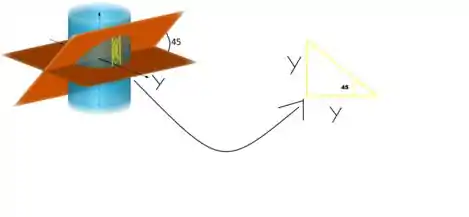
Em amarelo foi é um corte no sólido,sendo que está fatia tem a forma de um triângulo isósceles,como mostrado na imagem a direita.

Fazendo um corte nessa cunha, obteremos um triangulo isósceles com área igual a

A x = b a s e   x   a l t u r a 2    

A base é igual a y e a altura também será y por se tratar de um triângulo com dois lados iguais.

A = y ⋅ ( y ) 2

A = y 2 2

Passo 2

Iremos reescrever y em função de x, para isso usaremos Pitágoras:

y 2 + x 2 = r 2

y =   r 2 - x 2

Então, A ( x ) poderá ser reescrito como

A x = ( r 2 - x 2 ) 2

Passo 3

A integral ficará assim:

V = ∫ a b A ( x )   d x

V = 1 2 ∫ - r r r 2 - x 2   d x

Ou usando a simetria,

V = 2 2 ∫ 0 r r 2 - x 2   d x

= r 2 x - x 3 3 | 0 r

= r 2 r - r 3 3 - 0

= 2 r 3 3

Resposta

2 r 3 3

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Encontre o volume do sólido obtido pela rotação da região limitada pelas curvas dadas em torno das retas especificadas. Esboce a região, o sólido e um disco ou arruela típicos y = x 2 / 3 ,x = 1 ,y =
Encontre o volume do sólido obtido pela rotação da região limitada pelas curvas dadas em torno das retas especificadas. Esboce a região, o sólido e um disco ou arruela típicos. y 2 = x ,x = 2 y ;e mt
Encontre o volume do sólido obtido pela rotação da região limitada pelas curvas dadas em torno das retas especificadas. Esboce a região, o sólido e um disco ou arruela típicos y = 1 x ,y = 0 , x = 1 ,
Encontre o volume do sólido obtido pela rotação da região limitada pelas curvas dadas em torno das retas especificadas. Esboce a região, o sólido e um disco ou arruela típicos. y = x ,y = x ;e mt o r
Veja a figura e encontre o volume gerado pela rotação da região ao redor da reta dada. R 1e mt o r n od eO C