Enunciado
Cálculo - Cálculo com Geometria Analítica Volume 1 - 3ª Edição - Louis Leithold- Ed: 3º - Capítulo 4.9 - Ex. 4
- Encontre e para os valores indicados de e .
- Faça um esboço do gráfico e indique os segmentos de reta cujos comprimentos são e .
Passo 1
a) Para achar , vamos começar lembrando que se a função for definida por , então a diferencial de , denotada por será dada por onde está no domínio de e é um incremento arbitrário de . Então temos que:
Utilizando a definição acima, ficamos com:
Se , então:
Passo 2
Para achar (variação do , vamos utilizar que .
Se , então:
Passo 3
Segue o esboço do gráfico com todos dados indicados.
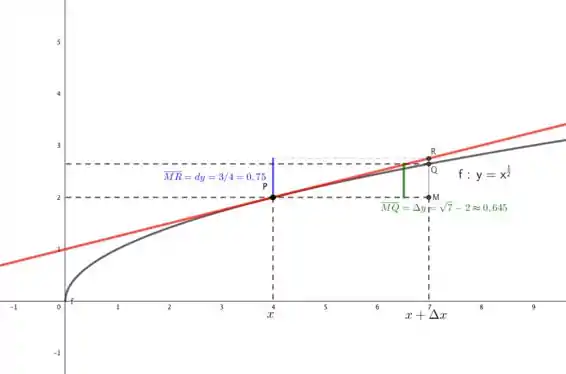
Olhando mais de perto
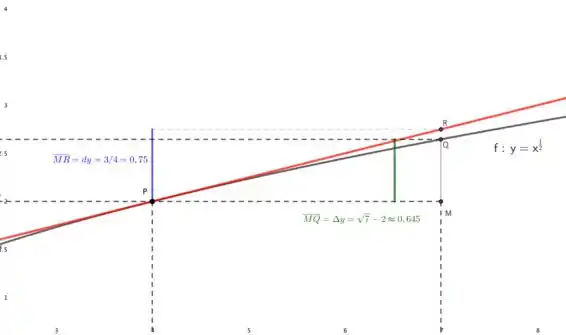
Para representar o , nós precisamos esboçar os pontos:
e .
é a diferença dos de cada ponto, ou seja, .
Para representar o podemos marcar um segmento de unidades acima do ponto igual acontece na imagem. Ou traçar a tangente no e achar o ponto de interseção da reta tangente com o prolongamento de , o segmento .
Resposta
- e .
Exercícios de Livros Relacionados
Seja A = l 2 , l0 .a) Calcule a diferencial.b) Interprete geometricamente o erro que se comete na aproximação de Δ A por d A . (Olhe para A = l 2 como a fórmula para o cálculo da área do quadrado de l
Seja V = 4 3 π r 3 . r0 .a) Calcule a diferencial.b) Interprete geometricamente d V .(Lembre-se que V é o volume da esfera de raio r e que 4 π r 2 é a área da superfície esférica de raio r .)
Nos exercícios de 25 a 30, x e y são funções de uma terceira variável. Calcule d y d x , encontrando o diferencial termo a termo (veja o Exemplo 3). 8 x 2 - y 2 = 32
Nos exercícios de 25 a 30, x e y são funções de uma terceira variável. Calcule d y d x , encontrando o diferencial termo a termo (veja o Exemplo 3). 3 t g 2 x + 4 sec 2 y = 1
Nos exercícios de 25 a 30, x e y são funções de uma terceira variável. Calcule d y d x , encontrando o diferencial termo a termo (veja o Exemplo 3). 2 x 2 y - 3 x y 3 + 6 y 2 = 1