50. Uma partícula move-se ao longo do eixo , sua posição no instante dado por , onde está medindo em segundo e , em metros.
(a) Encontre a aceleração no instante . Quando ela está em ?
(b) Faça o gráfico das funções posição, velocidade e aceleração para .
(c) Quando a partícula está aumentando a rapidez? E quando está diminuindo?
Passo 1
Fala aí! tudo certinho?
Nesse problema foi dada uma função que representa a posição de uma partícula em função do tempo
E nosso objetivo é determinar o instante onde a aceleração é nula, esboçar o gráfico da função posição, velocidade e aceleração para entre e e por fim, temos que determinar quando a partícula está aumentando a rapidez e quando está diminuindo.
Bastante coisa, né?
Lá da física, a gente sabe que a derivada do espaço em relação ao tempo é a velocidade:
e a derivada da velocidade em relação ao tempo é a aceleração:
Então precisamos derivar duas vezes a função fornecida no enunciado:
Assim, como é uma fração de funções vamos aplicar a regra do quociente que é definida por
Bora lá!
Passo 2
Vamos calcular a função velocidade derivando a função
Usando regra da divisão:
A derivadas são apenas de polinômios:
Derivando mais uma vez, para obtermos a aceleração:
Podemos colocar o em evidência em cima, para cortar em cima e embaixo:
Deixando o em evidência:
Então a função da aceleração é
Tranquilo até aqui?
Passo 3
O enunciato nos pede o tempo quando , então:
Então
Ou
Como o tempo não pode ser negativo, os dois instantes de tempo em que a aceleração é igual a zero são:
e
Bacana, não é?
Passo 4
Podemos usar o GeoGebra para desenhar o gráfico com as funções já que a função nos permitiu usar alguma ferramenta gráfica nesse item.
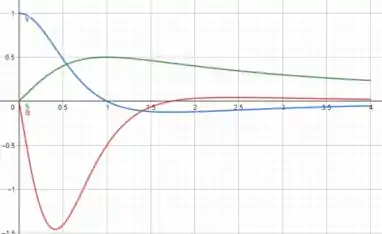
A azul indica a posição;
A verde a velocidade;
E a vermelha a aceleração.
Show?
Passo 5
A partícula aumenta a rapidez quando ela tem a velocidade e a aceleração com mesmo sinal.
Isso ocorre em
É isso! O que achou? Responde Aí!
Resposta
(a)
em dois instantes: e
(b)
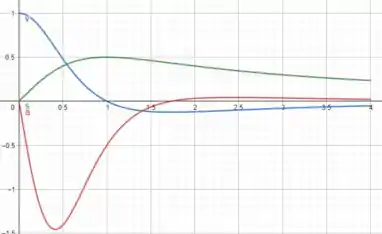
(c)