Enunciado
Cálculo - Cálculo Volume 1 - 5ª Edição - James Stewart- Ed: 5º - Capítulo 3.7 - Ex. 2
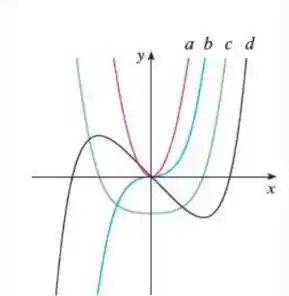
2. A figura mostra os gráficos de f, f’, f’’ e f’’’. Identifique cada curva e explique sua escolha.
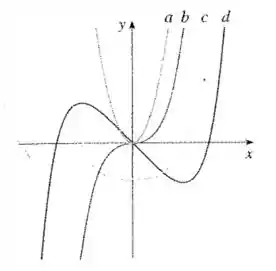
Passo 1
Olá, meu amigo. Yuri aqui e estarei te ajudando a resolver essa atividade.
Aqui iremos, eu e você, descobrir qual gráfico corresponde a tal derivada.
Tem duas coisas que podemos analisar para descobrir rapidamente qual função é derivada de qual:
- Na coordenada em que uma função atinge seu mínimo ou máximo local a derivada cruza o zero.
- Quando uma função está decrescendo (tangente negativa) sua derivada é negativa e quando ela está crescendo (tangente positiva) a derivada é positiva.
Se isso não for o suficiente, podemos observar também que:
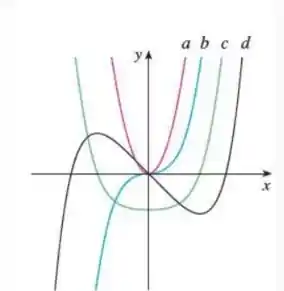
Passo 2
Quando atinge seus máximos e mínimos locais, apenas a função assume o valor zero, ou seja é a derivada de ⇒ .
A função nunca para de crescer então sua derivada é sempre positiva, a única função que é sempre positiva é ⇒ .
As funções e possuem tangentes negativas para e apenas o gráfico é todo negativo quando , mas como a gente sabe que não pode ser a derivada de , porque . Podemos dizer que
Então
