Enunciado
Cálculo - Cálculo Volume 2 - 5ª Edição - James Stewart- Ed: 5º - Capítulo 9.4 - Ex. 18
a) Se são emprestados a de juros, calcule as quantidades devidas no final de dois anos se os juros forem compostos (i) anualmente, (ii) trimestralmente, (iii) mensalmente, (iv) diariamente, (v) por hora e (vi) continuamente.
b) Suponha que sejam emprestados e os juros sejam compostos continuamente. Se for a quantidade devida depois de anos, onde , plote para cada uma das taxas de juros , e na mesma tela.
Passo 1
Esse é um problema sobre juros compostos. A expressão genérica que vamos usar é
onde é o valor inicial, é a taxa de juros, é o tempo em anos e é o número de vezes que a taxa é aplicada ao longo de um ano!
Assim, nossa equação, em função de fica:
Passo 2
Se a taxa é aplicada anualmente (i), :
Já para a taxa trimestral (ii), :
Para rendimento mensal (iii), temos :
Para rendimento diário (iv), usamos :
E para rendimento por hora (v), temos :
Tomando o limite contínuo (vi):
Note que o rendimento por hora é praticamente igual ao rendimento contínuo pois o número de parcelas é muito grande!
Passo 3
No item (b) devemos considerar rendimento contínuo para três taxas diferentes:
A seguir plotamos as três curvas:
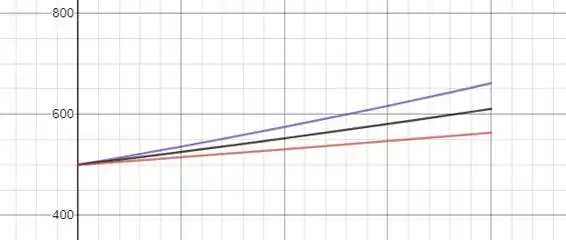
Quanto maior a taxa, maior o crescimento!