Enunciado
Cálculo - Anton - Cálculo - Vol 1- Ed: 10º - Capítulo 0.Revisão - Ex. 9
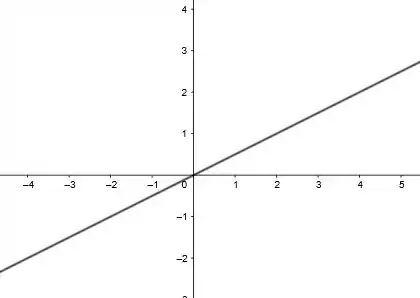
9. Obtenha o gráfico da equação .
Passo 1
Beleuza galeris, primeiro de tudo, antes de traçarmos o gráfico, podemos simplicar essa equação, saca só:
E tirando a raiz quadrada dos dois lados, temos:
Passo 2
Agora ficou que a equação ficou uma gracinha, podemos traçar o gráfico dela, vai ser dado por:
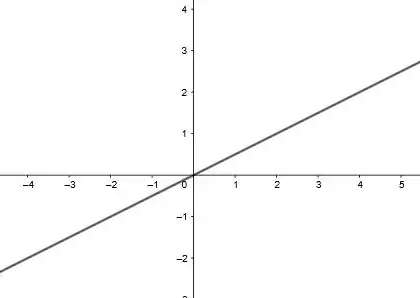
Resposta
Exercícios de Livros Relacionados
Em cada parte, compare os domínios naturais de f e de g f x = x 2 + x x + 1eg x = x f x = x x + x x + 1eg x = x
Encontre g (3) , g (- 1) , g (pi) , g (- 1,1) e g ( t^2 - 1 ) g (x) = (x + 1)/(x - 1) g (x) = {[[sqrt(x + 1) , x = 1],[3 , x1]])
Encontre f (0) , f (2) , f (- 2) , f (3) , f (sqrt(2)) e f ( 3 t ) f (x) = 3 x^2 - 2 f (x) = {[[(1)/(x) , x3],[2 x , x = 3]])
Determineasfórmulas paraf + g ,f - g , f g e f / g e obtenha os domínios das funções.27) f x = 2 x - 1 , g x = x - 1
Determineasfórmulas paraf + g ,f - g , f g e f / g e obtenha os domínios das funções.27) f x = x 1 + x 2 , g x = 1 x