Enunciado
Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 10.4 - Ex. 54
51-54. Use uma calculadora ou um computador para encontrar o comprimento do laço, com precisão de quatro casas decimais. Se necessário, use um gráfico para determinar o intervalo de parâmetro.
54.
Passo 1
Para determinarmos o comprimento da curva polar com equação , como é o nosso caso, precisamos determinar o resultado da seguinte integral, pessoal:
No qual é o comprimento que estamos procurando e o intervalo é o intervalo de parâmetro. Como o enunciado nos permite utilizar do gráfico para determinar esse intervalo, então é o que faremos! Plotando o gráfico dessa curva polar, teremos:
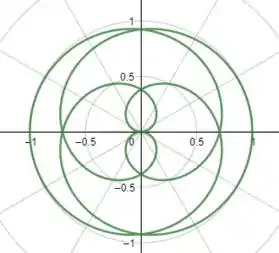
Simplificando o máximo possível o raciocínio, podemos dizer que o intervalo do parâmetro é o mínimo intervalo para que o gráfico da curva polar fique completo! Nesse caso, o intervalo será , se diminuirmos o intervalo a figura não ficará completa e se aumentarmos o intervalo não fará diferença no gráfico.
Passo 2
Por fim, o que falta é determinarmos , não é mesmo? Então bora derivar essa função aí! Se liga:
Utilizando a regra da cadeia, teremos:
Substituindo na integral:
Utilizando uma calculadora para determinar o resultado da integral, obteremos: