Enunciado
Cálculo - Cálculo Volume 1 - 5ª Edição - James Stewart- Ed: 5º - Capítulo 3.7 - Ex. 21
a) Se , encontre e .
b) Para ver se suas respostas para a parte (a) são razoáveis compare os gráficos de , e .
Passo 1
Iae, meus queridos! Está com dificuldades nessa questão? Não se preocupe! Estamos aqui para ajudar 😉
Nesse problema foi dada a função
E nosso objetivo é obter a primeira e a segunda derivada.
A partir das derivadas obtidas vamos plotar os gráficos de , e para compará-los usando uma ferramenta gráfica.
Parece complicado?
Para calcular a derivada de vamos ter que aplicar a regra da cadeia. Isso porque quando formos derivar o termo precisamos aplicar essa regra pois esse termo é uma função composta.
A regra da cadeia é dada por
Bora lá!
Passo 2
Vamos começar derivando a função
Aplicando a regra da cadeia em considerando como a função de dentro e como a função de fora sendo a função de dentro
Pelo teorema fundamental do cálculo, temos
E pela regra da potência
Substituindo em
Substituindo e simplificando a equação...
Tranquilo até aqui?
Passo 3
Com a primeira derivada em mãos, vamos calcular a derivada do resultado para obter a derivada de segunda ordem.
Nesse caso, temos um produto de funções, então podemos aplicar a regra do produto para calcular essa derivada.
Aplicando a regra à nossa função, temos
Pelo teorema fundamental do cálculo novamente, chegamos em
Bacana, não é?
Passo 4
Agora, vamos usar uma ferramenta gráfica para plotar os gráficos de , e
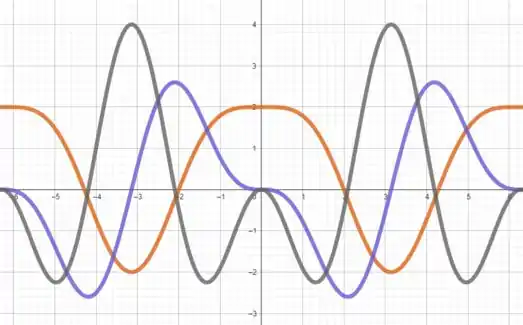
Em laranja temos , em roxo e em cinza . Perceba que nos pontos máximos e mínimos de uma função, sua derivada corta o eixo , isso porque a derivada da função naquele ponto é igual a (reta tangente é horizontal).
É isso, espero ter ajudado! Entendeu tudo? Responde Aí! 😎👍
Resposta
