Enunciado
Cálculo - Cálculo Volume 1 - 5ª Edição - James Stewart- Ed: 5º - Capítulo 3.7 - Ex. 22
22.
(a) Se , encontre e .
(b) Para ver se sua respostas para a parte (a) são razoáveis, compare os gráficos de e .
Passo 1
Fala aí! tudo certinho?
Nesse problema foi dada a função
E nosso objetivo é calcular , e platar os gráficos de , e com o auxilio de uma ferramenta gráfica.
Parece complicado?
Para calcular as derivadas dessa função temos que aplicar a propriedade da derivada da soma e aplicando o teorema fundamental do calculo (TFC) e a regra da potência calculamos as derivadas de .
A regra da potencia, caso não se lembre, é dada por
Sacou? Bora começar!
Passo 2
Calculando a derivada de , temos
Aplicando a propriedade da soma...
Pelo TFC temos que
E pela regra da potencia, temos
Substituindo em ...
Tranquilo até aqui?
Passo 3
Agora vamos calcular a segunda derivada de .
Pra isso vamos seguir os mesmos passos
Já sabemos qual é a derivada de e a derivada de é calculada pela regra da potencia como
Substituindo em
Show?
Passo 4
E agora, com o auxilio de uma ferramenta gráfica, vamos plotar os gráficos de , e .
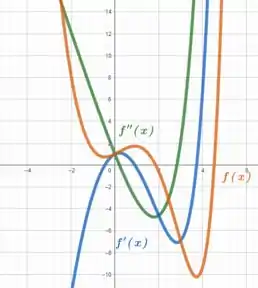
As funções são sim razoáveis, pois:
Quando atinge seus máximos e mínimos a fun��ão que calculamos como sendo sua derivada realmente se econtra no , como era de se esperar, além de que, quando está crescendo, é positiva e quando está decrescendo é negativo.
Já quando atinge seus máximos e mínimos está em e assim como com e com , quando está crescendo, é positiva e quando está decrescendo é negativo.
É isso! Entendeu tudo? Responde Aí!