Enunciado
Cálculo - Cálculo - 12ª Edição - Maurice D. Weir e Joel Hass (George B. Thomas)- Ed: 12º - Capítulo 1.3 - Ex. 57
57. Aplique a lei dos cossenos ao triângulo da figura a seguir para deduzir a fórmula para .
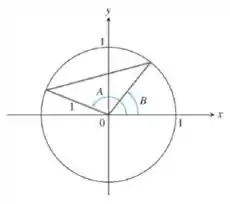
Passo 1
Pra começar, olha bem pra imagem do enunciado:
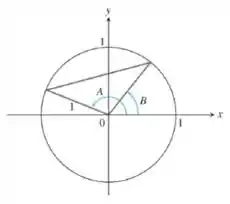
Nota o seguinte galera, se pegarmos o ângulo da figura e subtrairmos dele o ângulo , acabamos achando o ângulo :
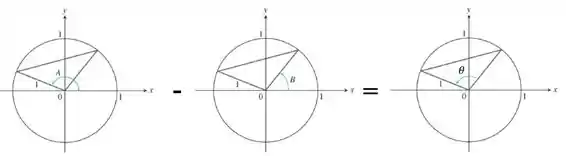
E destacando o triângulo grande que temos aí dentro:
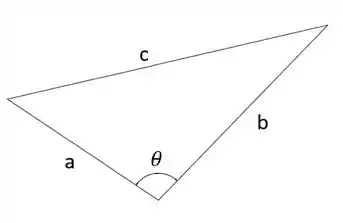
Show galera, é aqui que a lei dos cossenos entra! Pra esse triângulo vamos ter:
Vamos lembrar no entanto que esse triângulo está dentro de um círculo, de forma que tanto quanto são lados iguais ao raio do círculo. Como o raio é igual a e :
Agora só precisamos encontrar o valor de que a questão está resolvida.
Passo 2
Pra achar o valor de , a gente pode estabelecer pontos e tais que:
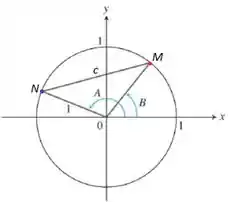
Assim, a distância entre esses dois pontos será o tamanho de . Primeiro pro ponto , olhando somente pro primeiro quadrante, temos:
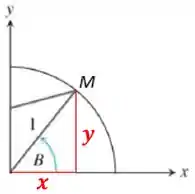
Da trigonometria:
Logo:
Na real na real a gente pode aplicar essa fórmula pra qualquer ponto sobre a circunferência, mesmo que ele esteja em outro quadrante. A única coisa que vai mudar é o ângulo. Ou seja, escrevendo as coordenadas de pontos como esses em função do ângulo, pro ponto , encontramos:
Duvida? Faça um teste pra um qualquer entre e , isto é, um ponto do segundo quadrante. Você verá que o cosseno desse ângulo é negativo e o seno positivo, confirmando a posição dele no segundo quadrante. O mesmo vale pro terceiro e quarto quadrante. Agora, calculando a distância entre esses pontos, temos:
Passo 3
Agora é só igualar o das duas equações encontradas. Respectivamente vindo do passo e do passo , temos:
Logo:
Juntando os termos ao quadrado do mesmo ângulo, temos:
E o interior desses colchetes será, pela relação trigonométrica, igual à . Logo:
Dividindo dos dois lados por :
Ta na mão!