Enunciado
Cálculo - Cálculo Volume 1 - 5ª Edição - James Stewart- Ed: 5º - Capítulo 2.7 - Ex. 6
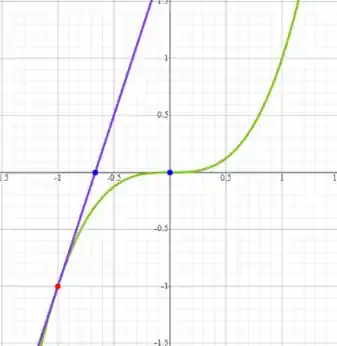
6. (a)Encontre a inclinação da reta tangente à curva no ponto
(i) Usando a Definição 1
(ii) Usando a Equação 2
(b) Encontre a equação da reta tangente da parte (a)
(c) Faça um gráfico da curva e da reta tangente em retângulo cada vez menores centrados no ponto até que a curva e a tangente fiquem não distinguíveis.
Passo 1
Fala aí, pessoal.
Essa questão deu pra gente a curva e pede para que a gente estude o comportamento da reta tangente a essa curva em diferentes situações que são pedidas em três itens diferentes.
No item a) devemos encontrar a inclinação dessa reta tangente em um ponto específico, o ponto , por dois meios diferentes. O primeiro é usando a definição 1 do livro e o segundo é usando a equação 2
No item b) encontraremos a equação dessa reta tangente.
E no item c) faremos o gráfico desta curva e da reta tangente em retângulo cada vez menores centrados no ponto até que a curva e a tangente fiquem não distinguíveis.
Vamos fazer uma coisa de cada vez, e pra isso vou dividir os itens em passos diferentes.
Vem que te ajudo nessa.
Passo 2
No item a) devemos encontrar a inclinação dessa reta tangente em um ponto específico, o ponto , por dois meios diferentes. O primeiro é usando a definição 1 do livro e o segundo é usando a equação 2
Lembrando de cada um dos métodos, temos:
Definição :
Em que , é o coeficiente angular da reta tangente à curva no ponto
E a equação
Em que , é o coeficiente angular da reta tangente à curva no ponto e .
Então, vamos lá!
O ponto de tangência é o ponto , então:
A questão já nos dá o
(i) Pela definição 1:
Fatorando o , pois se substituirmos o valor de na expressão acima, teremos uma indeterminação do tipo .
Podemos pensar nele como uma soma de cubos, fazendo
“Cortando” o no denominador (parte de baixo) e no numerador (parte de cima), temos:
E aplicando o limite, ficamos com:
Show, pela definição 1, o coeficiente angular da reta é .
Passo 3
(ii) Faremos agora pela equação e tem que dar o mesmo resultado hein! Serve até como prova real.
Assim:
Anotando algumas coisas para não nos enrolarmos:
isso foi dado no problema hein, não esquece:
Substituindo tudo no cálculo do limite temos:
Botando o em evidência, temos:
Cortando o de cima e de baixo, temos:
Obaaa! Deu igual, estamos pensando certo!
Passo 4
Vamos agora para o item b), onde devemos encontrar a equação dessa reta tangente.
A equação da reta tangente será:
Em que é o ponto de tangência.
Assim, já sabemos que e . Basta substituir tudo:
E a equaç��o será:
Passo 5
Para c) faremos o gráfico da curva e da reta tangente:
Para a curva temos:
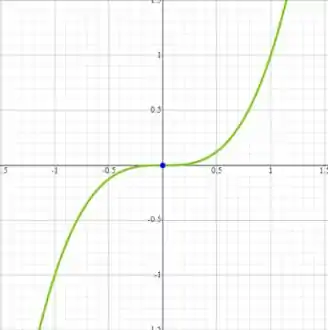
E a reta tangente a essa curva no ponto , que é dada pela equação:
Que corta o eixo em e o eixo em .
Assim o gráfico será:
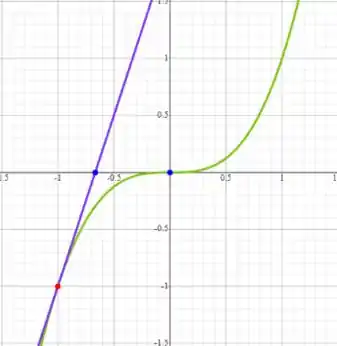
Resposta
()
(c)
