Enunciado
Cálculo - Cálculo Volume 1 - 6ª Edição - James Stewart- Ed: 6º - Capítulo 2.1 - Ex. 3
O ponto pertence à curva
- Se é o ponto , use sua calculadora para determinar o coeficiente da reta secante , com precisão de 6 casas decimais, para os seguintes valores de
- 0,5
- 0,9
- 0,99
- 0,999
- 1,5
- 1,1
- 1,01
- 1,001
- Usando os resultados da parte (a), estime o valor da inclinação da reta tangente à curva no ponto .
- Utilize a inclinação obtida na parte (b) para achar uma equação da reta tangente à curva em .
Passo 1
Fala aí! Vamos resolver essas questão juntinhos!
Aqui a gente tem uma curva:
E queremos achar o coeficiente angular da reta secante , sendo que:
Pra achar o coeficiente angular de uma reta quando temos 2 pontos, é bem simples, é só fazer a variação em sobre a variação em :
Já aplicando aos nossos valores:
Então basta a gente substituir os valores de dados pelo enunciado, pra achar o coeficiente angular de cada secante.
No item b, queremos a tangente em , então precisamos lembrar que a reta tangente só cruza a curva em um único ponto. Como a secante cruza a reta em 2 pontos, a gente poderia pensar que a tangente é uma secante em que . Então a gente pode aplicar um limite pra que:
E no item c, já tendo o coeficiente angular da tangente, basta encontrar o coeficiente linear pra completar a equação da reta:
Passo 2
Começando pela letra a, queremos os coeficientes angulares das secantes em que o do ponto assume os valores a seguir:
- 0,5
- 0,9
- 0,99
- 0,999
- 1,5
- 1,1
- 1,01
- 1,001
Então basicamente a gente substituir esses valores na equação que já achamos no passo 1:
- 0,5
- 0,9
- 0,99
- 0,999
- 1,5
- 1,1
- 1,01
- 1,001
Show! Essa já foi!
Passo 3
Agora vamos para a letra b, usando os valores que encontramos, vamos montar uma tabela:
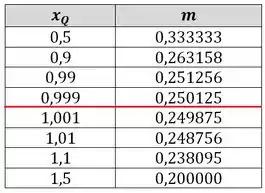
E temos que estimar o valor da inclinação da reta tangente.
Repara que os valores de vão se aproximando de , pela direita e pela esquerda. E isso é justamente o que queremos: o limite pra quando .
O valor ficaria exatamente na linha vermelha da tabela. Então, podemos olhar de qual valor está se aproximando nessa linha.
O valor abaixo é um pouquinho menor que 0,25 e o valor acima é um pouquinho maior que 0,25. Então estimamos que a inclinação da reta tangente em é:
ou
Passo 4
Para finalizar vamos resolver a letra c! Vamos achar uma equação para a reta tangente…
E como já temos ,
basta achar o . E pra isso podemos usar qualquer ponto da reta.
Só temos um ponto, então é ele mesmo o escolhido:
Vamos substituir:
𝐸ntão a reta tangente fica:
Uhul! Conseguimos!
