Enunciado
Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 2.1 - Ex. 9
O ponto está sobre a curva
Se for o ponto , encontre a inclinação da reta secante (correta até a quarta casa decimal) para As inclinações parecem tender a um limite?
Use um gráfico da curva para explicar por que as inclinações das retas secantes da parte (a) não estão próximas da inclinação da reta tangente em .
Escolhendo as retas secantes apropriadas, estime a inclinação da reta tangente em .
Passo 1
Olá, meu amigo. Yuri aqui e estarei te ajudando a resolver essa atividade.
Aqui a questão nos pede para calcularmos a inclinação das retas secantes PQ, sendo P um ponto fixo e Q um ponto dado pela equação .
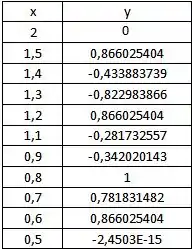
Primeiramente, calcularemos os valores de da função para cada dado, e iremos montar uma tabela para facilitar nossa visualização.
Assim, sabemos os valores dos pontos .
Depois para calcular a inclinação entre e , faremos:
Onde e são as coordenadas e do ponto e e as coordenadas e do ponto .
Passo 2
Encontrando os valores de do ponto , por exemplo para , temos:
Para temos:
E faremos isso para os valores de dados.
Agora, utilizando a fórmula da inclinação da reta secante.
Onde e são os intervalos onde queremos encontrar a inclinação da reta secante.
Sabemos que foi dado , então, substituindo em ficamos com
Entao, agora podemos construir uma tabela com todos os valores calculados, basta substituirmos por cada valor de dado no enunciado e por cada associado aos respectivos valores de dados (os valores calculados na tabela acima).
Por exemplo, para , temos , logo:
Para , temos , logo:
Fazendo para os demais valores, obtemos:
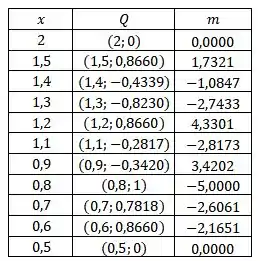
As inclinações não parecem tender a um limite quando
Passo 3
Esboçando o gráfico da curva
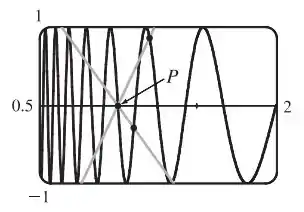
Podemos ver que as inclinações das retas secantes não estão próximas da inclinação da reta tangente, pois o gráfico da função oscila muito rapidamente
Passo 4
Se pegarmos dois pontos muito próximos do ponto , nós conseguiremos ter uma aproximação razoável, então escolheremos e , calcularemos as inclinações das retas secantes e então calcularemos a inclinação da reta tangente.
Para
Calculando a inclinação da reta secante () e usando o ponto , ficamos com
Para
Calculando a inclinação da reta secante () e usando o ponto , ficamos com
Com isso, podemos ver que a inclinação da reta tangente (que é a média das inclinações das retas secantes) é igual a .
Resposta
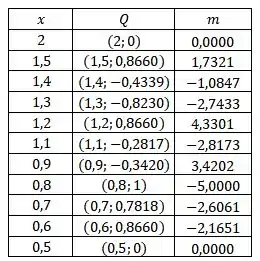
As inclinações das retas secantes não estão próximas da inclinação da reta tangente pois o gráfico da função oscila muito rapidamente.
A inclinação da reta tangente é