Enunciado
Cálculo - Cálculo Volume 1 - 5ª Edição - James Stewart- Ed: 5º - Capítulo 2.7 - Ex. 10
7-10. Encontre uma equação da reta tangente à curva no ponto dado.
7. ,
Passo 1
Olá, meu querido amigo. Estarei te ajudando a resolver essa atividade.
Aqui, iremos encontrar a equação da reta tangente a curva
E faremos isso no ponto
Da curva dada. Basicamente temos uma curva, e um ponto, gostaria de encontrar uma reta tangente a esta curva e que passe por esse ponto dado.
Veja que o ponto dado pelo enunciado não pertence a função, provavelmente um erro de digitação, o ponto que pertence a função em é
E é com ele que iremos trabalhar.
Primeiro, precisamos encontrar a inclinação da reta tangente à curva. Para isso, utilizaremos a equação:
Em que , é o coeficiente angular da reta tangente à curva no ponto e .
A equação da reta tangente será então:
Em que é o ponto de tangência, no nosso caso .
Passo 2
Primeiro vamos encontrar o coeficiente angular da nossa reta:
Lembrando que , vamos encontrar :
Substituindo os valores:
Realizando o produto notável:
Substituindo agora tudo na expressão do limite, temos:
Realizando o no numerador:
Agora organizando as frações:
Realizando as devidas contas no numerador:
“Cortando” o do numerador com o do denominador, temos:
Agora de fato calculando o limite:
Passo 3
Com o coeficiente angular da reta já calculado, vamos substituir o ponto e esse coeficiente na equação da reta tangente.
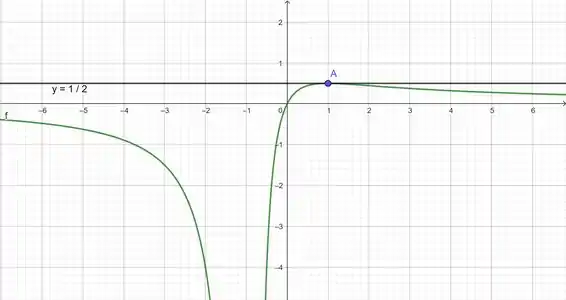
Abaixo veja o gráfico do que encontramos juntos, que confirma nosso acerto:
