Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Anton - Cálculo - Vol 1- Ed: 10º - Capítulo 6.1 - Ex. 10

7-18 Esboce a região englobada pelas curvas e encontra a área

10. y = sec 2 ⁡ x , y = 2 , x = - π 4 , x = π 4

Passo 1

Vamos começar falando a fórmula que vamos usar nessa questão e lembrando que depois, teremos que fazer o esboço das curvas!

Essa fórmula é a 6.1.2 Fórmula para a área

Se f e g forem contínuas no intervalo [ a , b ] e se f ( x ) ≥ g ( x ) em cada x de [ a , b ] , então a área da região limitada acima por y = f ( x ) , abaixo por y = g ( x ) , à esquerda pela reta x = a e à direita pela reta x = b é

A = ∫ a b f x - g ( x ) d x

Passo 2

O esboço da região é assim:

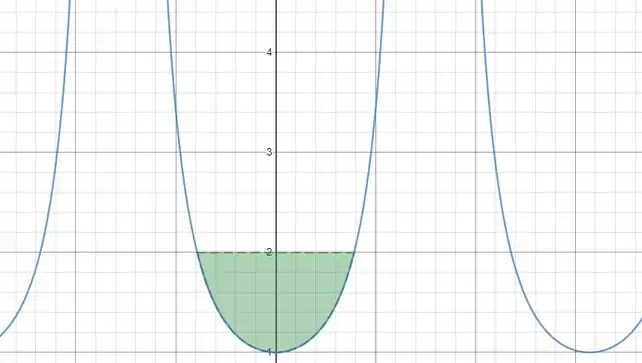
A curva é limitada acima por f x = 2 e abaixo é limitada por g x = sec 2 ⁡ x , à esquerda é delimitada pela reta x = - π 4 , então a = - π 4 e à direita é delimitada por x = π 4 , então b = π 4 .

Montando nossa integral da área, ela fica assim:

A = ∫ - π 4 π 4 ( 2 - ⁡ sec 2 ⁡ x ) d x

Vamos calcular a integral indefinida abaixo:

∫ ( 2 - ⁡ sec 2 ⁡ x ) d x = ∫ 2 d x - ∫ sec 2 ⁡ x d x

Vamos calcular em separado cada uma:

∫ 2 d x = 2 x + C

∫ sec 2 ⁡ x d x = tan ⁡ x + C

Voltando para a integral, temos, lembrando que essa integral ∫ sec 2 ⁡ x d x vai com o sinal negativo:

∫ ( 2 - ⁡ sec 2 ⁡ x ) d x = 2 x - tan ⁡ x + C

Passo 3

Vamos pegar a antiderivada abaixo

F x = 2 x - tan ⁡ x

Então para calcularmos a integral definida:

A = ∫ - π 4 π 4 ( 2 - ⁡ sec 2 ⁡ x ) d x = F π 4 - F ( - π 4 )

Calculando F π 4 e F ( - π 4 ) :

F π 4 = 2 π 4 - tan ⁡ π 4 = π 2 - 1

F - π 4 = 2 - π 4 - tan ⁡ - π 4 = - π 2 - 1

Voltando para a expressão da área, temos:

A = ∫ - π 4 π 4 ( 2 - ⁡ sec 2 ⁡ x ) d x = π 2 - 1 - - π 2 - 1 = π 2 - 1 + π 2 + 1 = π 2 + π 2 = π

Então:

A = π

Resposta

π

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Ache o centro de massa da lâmina limitada pela parábola 2 y 2 = 18 - 3 x , pelo eixo y , se a densidade superficial de massa em qualquer ponto ( x , y ) for 6 - xk g / m ² ².
Nos exercícios de 7 a 14, ache o centróide da região com os contornos indicados. (7) A parábola y = 4 - x ² ² e o eixo x .
Nos exercícios de 7 a 14, ache o centróide da região com os contornos indicados. (8) A parábola x = 2 y - y ² ² e o eixo y .
Nos exercícios de 7 a 14, ache o centróide da região com os contornos indicados. (9) A parábola y = x ² ² e a reta y = 4 .
Nos exercícios de 7 a 14, ache o centróide da região com os contornos indicados. (10) A parábola y ² = 4 x ² , o eixo y e a reta y = 4 .