Enunciado
Cálculo - Cálculo com Geometria Analítica Volume 1 - 3ª Edição - Louis Leithold- Ed: 3º - Capítulo 6.5 - Ex. 15
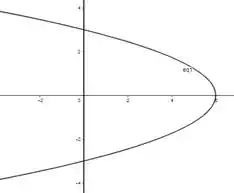
Ache o centro de massa da lâmina limitada pela parábola , pelo eixo , se a densidade superficial de massa em qualquer ponto for .
Passo 1
A lâmina é simétrica em relação ao eixo e a desenidade superficial não é uma função de , entao .
Passo 2
Calculando agora o valor de e .
Passo 3
Vamos agora encontrar agora os pontos do centróide.
Resposta
O centro de massa está localizado no ponto
Exercícios de Livros Relacionados
Determine o centro de massa da região A dada por 4 x 2 + y 2 ≤ 4 , y ≥ 0 . (Sugestão: Para o cálculo de x c aproveite a simetria da figura.)
Seja A o conjunto do plano de todos os ( x , y ) tais que 0 ≤ a ≤ x ≤ b , 0 ≤ f x ≤ y ≤ g ( x ) , onde f e g são supostas contínuas em [ a , b ] . Image A como uma lâmina delgada, homogênea, de modo q
Esboce a região delimitada pelas curvas indicadas e encontre sua área. y = 12 - x 2 , y = x 2 - 6
Esboce a região delimitada pelas curvas indicadas e encontre sua área. x = 2 y 2 , x = 4 + y 2
Esboce a região delimitada pelas curvas indicadas e encontre sua área. y = e x , y = x e x ,x = 0