Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Anton - Cálculo - Vol 1- Ed: 10º - Capítulo 6.1 - Ex. 18

7-18 Esboce a região englobada pelas curvas e encontra a área

18. y = x , y = 4 x , y = - x + 2

Passo 1

Vamos começar falando a fórmula que vamos usar nessa questão:

Essa fórmula é a 6.1.4 Fórmula para a área trocando x por y

Se w e v forem contínuas e w ( y ) ≥ v ( y ) em cada y de [ c , d ] , então a área da região limitada à esquerda por x = v ( y ) , à direita por x = w ( y ) , acima por y = d   e abaixo pela reta   y = c .

A = ∫ c d w ( y ) - v ( y ) d y

Podemos desenhar o gráfico e assim descobrir as propriedades que limitam essa curva!

Vamos isolar o y em todas as funções:

A primeira não precisa!

Na segunda, temos:

y = 4 x

x = y 4

Na terceira, temos:

y = - x + 2

2 - y = x

Passo 2

Vamos começar desenhando nosso gráfico para assim vermos como a região é delimitada!

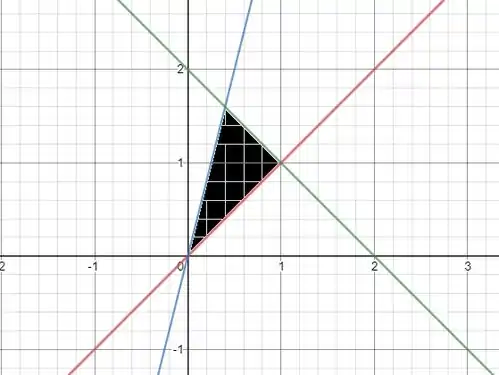
Em vermelho está a curva x = y ,em azul está a função x = y 4 e x = 2 - y está em verde, nós queremos a região em preto, para isso faremos a área delimitada da região entre as retas verde e azul menos a área da região entre as retas vermelho e azul

Começaremos pela região entre as retas x = y 4 e x = 2 - y

Quem delimita á direita é a função x = 2 - y , à esquerda é x = y 4 . Para nossa integral, temos:

w y = 2 - y

v y = y 4

Agora precisamos descobrir quem delimita acima e abaixo, abaixo quem delimita é a reta y = 0 para descobrirmos quem delimita acima, vamos igualar as duas funções:

2 - y = y 4

8 - 4 y = y

8 = 5 y

y = 8 5

Então quem delimita acima é y = 8 5   , portanto d = 8 5 para a nossa integral e quem delimita abaixo é y = 0 , então c = 0 .

Montando nossa integral, temos:

A 1 = ∫ 0 8 / 5 2 - y - y 4 d y = ∫ 0 8 / 5 2 - 5 y 4 d y

Agora faremos a região x = y e x = 2 - y

Quem delimita á direita é a função x = 2 - y , à esquerda é x = y . Para nossa integral, temos:

w y = 2 - y

v y = y

Agora precisamos descobrir quem delimita acima e abaixo, abaixo quem delimita é a reta y = 0 para descobrirmos quem delimita acima, vamos igualar as duas funções:

2 - y = y

2 = 2 y

1 = y

y = 1

Então quem delimita acima é y = 1   , portanto d = 1 para a nossa integral e quem delimita abaixo é y = 0 , então c = 0 .

Montando nossa integral, temos:

A 2 = ∫ 0 1 2 - y - y d y = ∫ 0 1 2 - 2 y d y

A nossa área é a diferença entre A 1 e A 2 .

A = A 1 - A 2

A = ∫ 0 8 / 5 2 - 5 y 4 d y - ∫ 0 1 2 - 2 y d y

Passo 3

Paramos na expressão da integral, então voltaremos dela!

A = ∫ 0 8 / 5 2 - 5 y 4 d y - ∫ 0 1 2 - 2 y d y

Vamos fazer a integral separadamente!

∫ 0 8 / 5 2 - 5 y 4 d y = 2 y - 5 y 2 8 8 5 0 = 16 5 - 8 5 - 2 × 0 - 5 × 0 2 8 = 8 5

∫ 0 1 2 - 2 y d y = 2 y - y 2 1 0 = 2 ( 1 ) - ( 1 ) 2 - 2 0 - 0 2 = 1

Agora voltando para a expressão da área, temos:

A = 8 5 - 1 = 3 5

Resposta

A = 3 5

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

34. Ache a abscissa do centroide da região do exercício 32.
35. Uma partícula move-se ao longo de uma reta de forma que v c m s seja a velocidade da partícula, decorridos ts ; então v = t 2 - t + 1 t + 2 2 ( t 2 + 1 ) ache a fórmula da distância percorrida pel
93. Ache área da região no primeiro quadrante limitada pelo eixo y e pelas curvas y = sec 2 ⁡ xey = t g 2 x .
Ache a área da região limitada pela curva y = e x , pelos eixos x e y e pela reta x = 2 .
Ache a área da região limitada pela curva y = e x e pela reta que passa pelos pontos ( 0 ,1 ) e ( 1 ,e ) .