Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo - 12ª Edição - Maurice D. Weir e Joel Hass (George B. Thomas)- Ed: 12º - Capítulo 8.2 - Ex. 74

74. Volume Determine o volume do sólido formado pela rotação da região delimitada pelos gráficos de y = s e n   x + sec ⁡ x , y = 0 , x = 0 e x = π 3 em torno do eixo x.

Passo 1

Para determina o volume dessa região primeiro precisamos calcular a integral desse gráfico

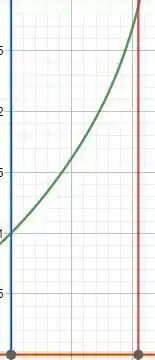
Pois ele é a curva que vai rotacionar para formar nosso sólido, e como ela rotaciona temos que multiplicar por π

Passo 2

Vamos calcular essa integral então

V = ∫ 0 π 3 π ( s e n   x + sec ⁡ x ) 2 d x = π ∫ 0 π 3 ( s e n 2 x + 2 ⋅ s e n   x ⋅ sec ⁡ x + sec 2 ⁡ x ) d x

Passo 3

Agora vamos calcular as integrais separadamente, começando por

∫ 0 π 3 ( s e n 2 x ) d x

Aqui precisamos lembrar que

s e n 2 x = 1 - cos ⁡ 2 x 2

Então basta fazer

∫ 0 π 3 ( s e n 2 x ) = ∫ 0 π 3 1 2 + ∫ 0 π 3 cos ⁡ 2 x 2 = [ 1 2 ⋅ x + 1 4 ⋅ s e n   2 x ] 0 π 3 = π 6 + 3 8

Passo 4

Agora temos que calcular essa integral

∫ 0 π 3 2 ⋅ s e n   x ⋅ sec ⁡ x d x

Basta lembrar que

sec ⁡ x = 1 cos ⁡ x

E aí podemos fazer uma substituição onde

u = cos ⁡ x d u = - s e n   x   d x

E nossa integral fica

∫ 1 1 2 2 - 1 u d u = 2 ⋅ ln ⁡ 2

Passo 5

Agora a última integral

∫ 0 π 3 ( sec 2 ⁡ x ) d x

Aqui precisamos fazer a substituição

u = tan ⁡ x

d u = sec 2 ⁡ x

E aí vemos que

∫ 0 π 3 ( sec 2 ⁡ x ) d x = [ tan ⁡ x ] 0 π 3 = √ 3

Passo 6

Agora vamos calcular

π ∫ 0 π 3 ( s e n 2 x + 2 ⋅ s e n   x ⋅ sec ⁡ x + sec 2 ⁡ x ) d x = π ⋅ [ π 6 + 3 8 + 2 ⋅ ln ⁡ 2 + √ 3 ]    

Resposta

π ⋅ [ π 6 + 3 8 + 2 ⋅ ln ⁡ 2 + √ 3 ]

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Utilize a tabela de integrais no fim do livro para calcular a integral ∫ sin 6 ⁡ 2 x d x
Use um sistema de computação algébrica para calcular a integral. Compare a resposta com o resultado usando as tabelas. Se as respostas forem diferentes, mostre que elas são equivalentes. ∫ sec 4 ⁡ x d
Use um sistema de computação algébrica para calcular a integral. Compare a resposta com o resultado usando as tabelas. Se as respostas forem diferentes, mostre que elas são equivalentes. ∫ sin 3 ⁡ x c
Calcule a integral. ∫ t g 3 xd x
Calcule a integral. ∫ s e n 3 x cos ⁡ xd x