Enunciado
Cálculo - Cálculo - 12ª Edição - Maurice D. Weir e Joel Hass (George B. Thomas)- Ed: 12º - Capítulo 5.4 - Ex. 83
83. Suponha que seja a função derivável mostrada no gráfico a seguir e que a posição no instante (segundos) de uma partícula que se desloca ao longo de um eixo coordenado seja
Metros. Use o gráfico para responder às seguintes perguntas. Justifique suas respostas.
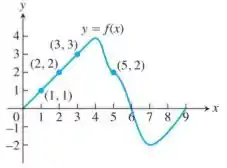
a. Qual é a velocidade da partícula no instante ?
b. A aceleração da partícula no instante é positiva ou negativa?
c. Qual é a posição da partícula no instante ?
d. Em que instante, durante os primeiros segundos, apresenta seu valor mais alto?
e. Quando, aproximadamente, a aceleração é zero?
f. Quando a partícula se desloca para a origem? E se afasta da origem?
g. De que lado da origem a partícula se situa no instante ?
Passo 1
a) Então galera, como a questão nos fornece a função da posição, podemos utilizar o teorema fundamental do cálculo para determinar a velocidade! Sabemos que a derivada da posição nos fornece a velocidade, certo? Ademais, segundo o T.F.C, temos:
Agora que encontramos uma expressão para a velocidade, para , de acordo com o gráfico, a vale , portanto:
Passo 2
b) A derivada no instante é uma reta decrescente, certo? Sendo assim, podemos concluir que a aceleração é negativa nesse ponto! Essa análise faz sentido porque o gráfico realmente está decrescendo, o que implica que a partícula está voltando para a origem.
Passo 3
c) Se olharmos o gráfico, conseguimos notar que até a partícula se move em M.R.U, certo? Se o movimento é uniforme, temos o seguinte:
Como a partícula sai do repouso, então , logo:
Em , , sendo assim:
Passo 4
d) Olhando o gráfico, temos que apresenta seu maior valor em , não é mesmo? Nesse instante de tempo, também, logo:
Passo 5
e) A aceleração da partícula é zero nos primeiros segundos, galera! Como assim, por que a aceleração é nula durante esse tempo? Como o movimento é uniforme nos primeiros segundos, então isso implica que a partícula não tem aceleração, o que difere dos outros intervalos de tempo, no qual há pequenas curvas no gráfico e, portanto, variações na velocidade.
Passo 6
f) De acordo com o gráfico, temos o seguinte, pessoal:
De a segundos a partícula está se: afastando da origem;
De a segundos a partícula está se: aproximando da origem;
De a segundos a partícula está se: afastando da origem;
De a segundos a partícula está se: aproximando da origem.
Passo 7
g) Se olharmos para o gráfico, podemos notar que centésimos antes dos segundos a partícula está voltando para a origem, uma vez que ela estava contra a trajetória (. Sendo assim, podemos concluir que momentos antes da partícula chegar em segundos de percurso ela estava no lado negativo da origem.
Resposta
a)
b) Negativa.
c)
d)
e) De a segundos.
f) De a e de a está se afastando;
De a e de a está se aproximando.
g) Lado esquerdo (negativo) da origem.