Enunciado
Cálculo - Cálculo Volume 1 - 5ª Edição - James Stewart- Ed: 5º - Capítulo 5.4 - Ex. 15
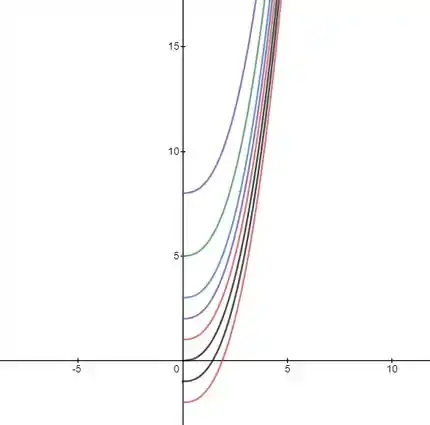
Ache a integral indefinida geral. Ilustre fazendo o gráfico de vários membros da família na mesma tela.
Passo 1
Olá, meu amigo. Estarei te ajudando a resolver essa integração.
A integral que ele nos pede para calcular é a seguinte:
Podemos reescrever a integral da seguinte forma:
Nesse caso, temos que lembrar do seguinte:
Quando
Passo 2
Integrando, temos:
Logo,
Pra finalizar, vamos fazer o gráfico e para vários valores de . Olha só:
Resposta
Exercícios de Livros Relacionados
64- Seja F (x) = int_(sqrt(3))^x a r c t g t d t . Encontrea)F ( sqrt(3) ) b) F ´ ( sqrt(3) ) c) F ´ ´ ( sqrt(3) )
59-62 Use a parte 2 do Teorema Fundamental do Cálculo para encontrar as derivadas.62- d d u ∫ 0 u xd x
59-62 Use a parte 2 do Teorema Fundamental do Cálculo para encontrar as derivadas.60- a) d d x ∫ 0 x d t 1 + t b)d d x ∫ 1 x ln t d t
63- Seja F (x) = int_4^x sqrt(t^2 + 9) d t . Encontrea)F ( 4 ) b) F ´ ( 4 ) c) F ´ ´ ( 4 )
65- Seja F x = ∫ 0 x t - 3 t 2 + 7d t para - ∞x+ ∞ .a)Encontre o valor de x para que F atinge seu valor mínimo.b)Encontre os intervalos nos quais F é somente crescente ou somente decrescente.c) Encont