Enunciado
Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 11.2 - Ex. 12
9-14. Calcule pelo menos dez somas parciais da série. Faça o gráfico de ambas as sequências de termos e de somas parciais na mesma tela. Parece que a série é convergente ou divergente? Se ela for convergente, calcule a soma. Se for divergente, explique por quê.
12.
Passo 1
Então pessoal, a questão nos pede várias coisas, então vamos tratar a questão com calma, passo a passo, ok? De início, o enunciado nos pede para calcular pelo menos dez somas parciais da série. Para calcularmos essas somas parciais, devemos fazer:
Mas o que seriam esses termos? De forma genérica, temos que uma série é descrita da seguinte forma:
No qual é sua n-ésima soma parcial e é a sequência de termos. No nosso caso, temos:
Passo 2
Botando em prática o conceito abordado no passo anterior, teremos:
Passo 3
Ok, descobrimos as dez somas parciais da série, galera! Antes de plotarmos o gráfico vamos prestar atenção na sequência dos termos . Concorda que a expressão se parece muito com uma série geométrica? Uma série geométrica tem o seguinte formato:
No qual é a relação comum e é o primeiro termo da sequência. Se , a série é divergente. Caso contrário, se , então a série é convergente e sua soma é:
Se manipularmos , teremos:
Disso tiramos que , então a série é convergente.
Passo 4
Já tivemos spoiler no passo anterior, mas se plotarmos o gráfico, teremos:
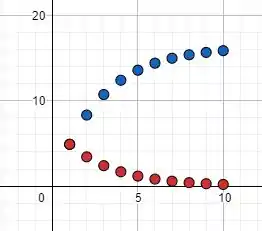
No qual os pontos em azul são referentes às somas parciais da série e os pontos em vermelho são referentes aos valores da sequência de termos. Pelo gráfico podemos notar que os pontos da sequência de termos se aproxima de , o que é um indicativo de que a série é convergente. Ademais, os pontos das somas parciais tendem a um valor específico, que é em torno de , aproximadamente, que é mais um indicativo de que a série é convergente. Por fim, se calcularmos a soma da série, teremos:
Que é mais uma prova de que, de fato, a série é convergente.