Enunciado
Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 10.6 - Ex. 9
9-16. (a) Encontre a excentricidade, (b) identifique a cônica, (c) dê uma equação da diretriz e (d) esboce a cônica.
Passo 1
A equação polar com foco na origem tem o seguinte formato, segundo a seção 10.6 do Stewart:
No qual é a excentricidade e é a diretriz da cônica em questão. Se associarmos um desses formatos com o da questão que nos foi dada, teremos que o que se assemelha é:
Passo 2
a) A equação que nos foi dada é a seguinte:
Se dividirmos todos os termos por , teremos:
Se fizermos uma comparação com a equação do passo 1, teremos:
Passo 3
b) De acordo com a seção 10.6 do Stewart, temos que:
Como no nosso caso e esse valor é menor do que , ou seja:
Então a nossa cônica é uma elipse.
Passo 4
c) A nossa equação tem denominador escolhido como , não é mesmo? Nesse caso, isso implica que a diretriz escolhida é da seguinte forma:
Como , e sabemos que é positivo, então . Nesse caso, nossa diretriz será:
Passo 5
d) Se esboçarmos a cônica, teremos:
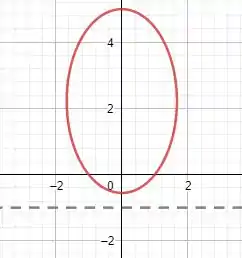
Resposta
