Enunciado
Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 10.5 - Ex. 41
Encontre a equação para a cônica que satisfaz as condições dadas.
41. Elipse, centro , vértice , foco
Passo 1
Oiii, tudo tranquilinho?? Bom... o enunciado quer que encontremos a equação para uma cônica.
Para isso, ele nos dá três condições:
- Trata-se de uma elipse;
- Possui focos em e ;
- Tem vértices em .
Para resolvermos isso, temos que saber do que trata-se uma elipse:
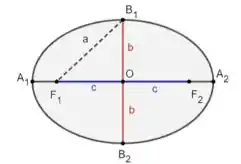
- é o centro da elipse;
- e são seus focos;
- e são as extremidades do eixo horizontal (vértices);
- e são as extremidades do eixo vertical (vértices);
- é a distância entre e ;
- é a distância entre e ;
- é a distância entre e .
Também sabemos que a elipse tem a seguinte equação para quando está centrada na origem e possui vértices na horizontal:
Masss, pelo que nos foi dado no enunciado, sabemos que os focos e os vértices pertencem ao eixo .
Assim, portanto, a elipse será do seguinte tipo:
Passo 2
Como o centro não está na origem, sabemos que a elipse está transladada, pela definição do vértice , podemos encontrar
Pegamos o valor negativo de , pois o vértice se encontra abaixo do centro.
Como o vértice e o foco estão no mesmo eixo paralelo ao eixo , equação da elipse terá a seguinte forma:
Passo 3
Para encontrarmos , vamos utilizar a definição do foco , para acharmos :
E pela equação de :
Podemos calcular :
Substituindo na equação da elipse: