Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Diva Flemming - Cálculo A- Ed: 6º - Capítulo 2.10 - Ex. 5

Se f x = x 2 + 2 x , achar f a + h - f ( a ) h , h ≠ 0 , e interprete o resultado geometricamente.

Passo 1

Tá, vamos substituir primeiro os valores e fazer f a e   f ( a + h ) :

f a = a 2 + 2 a

f a + h = a + h 2 + 2 ( a + h )

Passo 2

Beleza, agora vamos substituir na relação lá:

f a + h - f ( a ) h = a + h 2 + 2 a + h - ( a 2 + 2 a ) h  

a 2 + 2 a h + h 2 + 2 a + 2 h - a 2 - 2 a h

h 2 + 2 a h + 2 h h

= h + 2 a + 2

Passo 3

Vamos ver esse resultado geometricamente agora:

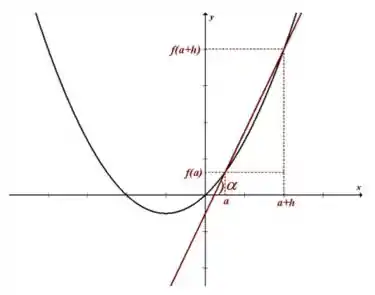
O quociente encontrado então é a tangente do ângulo entre o eixo x e a curva da função.

Resposta

h + 2 a + 2

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Dê o domínio e esboce o gráfico.r ) y = sqrt(x - 1)
Dê o domínio e esboce o gráfico.s ) y = sqrt(x + 2)
Dê o domínio e esboce o gráfico.n ) y = (1)/(( x + 1 )^2)
Dê o domínio e esboce o gráfico.o ) y = 1 + (1)/(x^2)
Dê o domínio e esboce o gráfico.l ) f (x) = (1)/(( x - 1 )^2)