Enunciado
Cálculo - Um curso de Cálculo Volume 1 - 5ª Edição - Hamilton Luiz Guidorizzi- Ed: 5º - Capítulo 2.1 - Ex. 15r
Dê o domínio e esboce o gráfico.
Passo 1
Essa função é do tipo racional do tipo:
E seu domínio é dado por:
No nosso caso temos e daí o a condição de existência vai ser:
Daí temos que:
E o domínio pode ser escrito como:
Passo 2
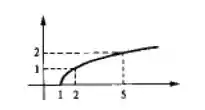
Vamos ao esboço? Vamos ver qual é a raiz dessa função:
Então a função cruza o eixo no ponto .
Outros pontos que satisfazem a função são:
Os pontos que temos são: e . Vamos ao esboço?
Passo 3
Colocando todos esses pontos num gráfico temos:
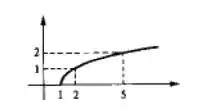
Resposta
Exercícios de Livros Relacionados
As funções f eg são definidas. Defina as seguintes funções e determine o domínio da função resultante g / f f x = x; g x = x 2 - 1
As funções f eg são definidas. Defina as seguintes funções e determine o domínio da função resultante f ∙ g f x = x + 1 x - 1 ; g x = 1 x
As funções f eg são definidas. Defina as seguintes funções e determine o domínio da função resultante f - g f x = x; g x = x 2 - 1
As funções f eg são definidas. Defina as seguintes funções e determine o domínio da função resultante f - g f x = | x |; g x = | x - 3 |
As funções f eg são definidas. Defina as seguintes funções e determine o domínio da função resultante f + g f x = x; g x = 4 - x 2