Enunciado
Cálculo - Cálculo com Geometria Analítica Volume 1 - 3ª Edição - Louis Leithold- Ed: 3º - Capítulo 6.4 - Ex. 19
Achar a massa total e o centro de massa.
19. A medida da densidade linear em qualquer ponto de uma barra com 6 m varia diretamente com a distância do ponto a um ponto externo na reta suporte da barra e a 4 m de um extremo, onde a densidade é 3 kg/m
Passo 1
O primeiro passo aqui é encontrar a densidade, e para isso analisaremos a figura abaixo.
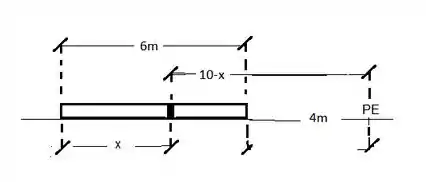
O exercício nos diz que a densidade da barra é proporcional a distância de um ponto qualquer a um ponto externo a 4 metros do extremo, e então o ponto qualquer estrá localizado a metros. Então podemos escrever nossa densidade da seguinte forma:
Passo 2
O exercício nos da outra informação também, sendo ela a seguinte:
- A densidade no extremo é 3 kg/m. com isso temos que .
Dessa forma podemos encotrar a constnte que permite que seja possível a igualdade do passo anterior.
Agora que achamos a contante podemos escrever de fato nossa densidade.
agora que sabemos a função da densidade podemos ir atrás da massa total e centro de massa.
Passo 3
Agora para achar a massa total usaremos a seguinte relação:
Onde nessa equação 𝞀 é a densidade do corpo e l é o comprimento da barra.
Com isso temos que a massa total pode ser expressa pela seguinte relação:
Isso é, a massa total vai ser a integral da densidade.
Achamos então a massa total da barra.
Passo 4
Para achar o centro de massa usaremos a seguinte relação:
Onde l é o comprimento da barra e é a densidade.
Portanto temos a seguinte equação para o centro de massa:
Resposta
Massa total:
Centro de massa: