Enunciado

Cálculo - Cálculo com Geometria Analítica Volume 1 - 3ª Edição - Louis Leithold- Ed: 3º - Capítulo 4.2 - Ex. 10

Ache a área do maior retângulo que possa ser inscrito numa circunferência dada de raio .

Passo 1

Essas questões têm um jeito bem metódico de resolver, saca só:

Precisamos de uma equação que associe a variável que queremos maximizar e outra variável do problema. Essa é normalmente a parte mais difícil do problema.
Depois que temos essa função, vamos encontrar a derivada dela e procurar os valores onde ela se iguala a e os valores onde ela não existe.
A partir do Teorema do Valor Extremo vamos encontrar os máximos e mínimos comparando os valores da função original nos extremos do intervalo e nos pontos onde a derivada é nula ou inexistente.

Passo 2

Esse problema é bem geométrico, então tem que dar uma visualizada no problema. Imagine que temos essa circunferência com um raio qualquer:

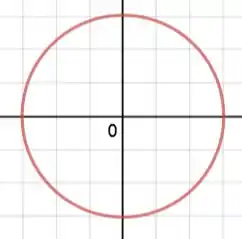
Essa circunferência pode ser descrita pela equação:

Agora imagine um retângulo aí dentro, desse jeito:

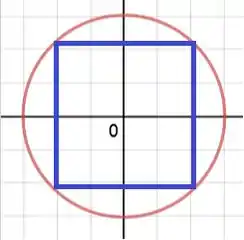
Imagine que esse retângulo tangencia um ponto genérico no primeiro quadrante. Vamos dividir o retângulo em quatro retângulos iguais menores e calcular a área de um desses retângulos. Depois é só multiplicar a área por ! As dimensões desse retângulo menor será de largura e de altura. A área total será:

Precisamos maximizar essa função, mas ela tem duas variáveis! Vamos pegar a outra equação que temos e isolar uma das variáveis em função da outra. Vamos elimina o da equação:

Tirando as raízes dos dois lados:

Mas estamos no 1º quadrante, onde o . Então podemos ficar só com a raiz positiva.

Agora podemos substituir isso na equação da área!

Agora sim temos a nossa função a ser maximizada. Ainda precisamos definir o nosso domínio. Como o retângulo está inscrito na circunferência, ele deve estar entre e o raio da circunferência. Eu disse que essa seria a parte mais difícil do problema hehe.