Compare as respostas dos seguintes problemas de construção
uma folha retangular com perímetro e dimensões será enrolada para formar um cilindro, como mostra a parte da figura. Que valores de e fornecem maior volume?
a mesma folha sofrerá revolução em torno de um dos seus lados de comprimento para formar outro cilindro, como indica a parte da figura. Que valores de e fornecem o maior volume?
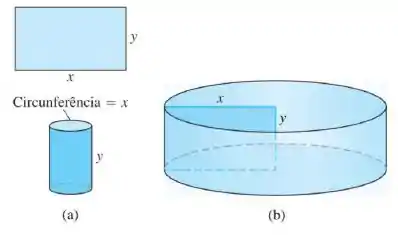
Passo 1
Letra
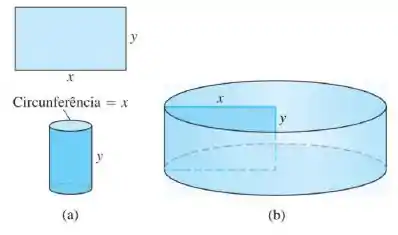
Ele disse que o perímetro é fixo, logo:
Vamos achar o volume em função de e de acordo com a forma que ele rodou.
Aqui na letra , a altura vai ser , enquanto vai ser o comprimento da base.
Assim, sendo o raio da base,
O volume vai ser:
Com
E
Assim, nosso volume fica:
Isolando o na equação do perímetro:
Vamos ter:
Onde o valor de vai de , até . Isso porque o não pode ser negativo e ele é menos
Passo 2
Para acharmos o valor de mínimo ou máximo, temos que comparar o valor da função nos pontos críticos e nos extremos do intervalo.
Primeiro fazemos:
Derivando ,
Fazendo isso igual a
Colocando em evidência:
Teremos:
Passo 3
Vamos achar o valor da função nos pontos críticos e extremos do intervalo:
Vamos ter:
O maior dos valores é quando
Então:
Passo 4
Vamos ajustar a fórmula do volume para o segundo caso agora:
O volume vai ser:
Com
E
Assim, nosso volume fica:
Isolando o na equação do perímetro:
Vamos ter:
É a mesma função de antes, so que com a variável , então ele vai maximizar em
E vamos ter:
Dessa forma, nas duas letras temos as mesmas dimensões da folha.