Enunciado
Cálculo - Cálculo - 12ª Edição - Maurice D. Weir e Joel Hass (George B. Thomas)- Ed: 12º - Capítulo 4.6 - Ex. 27
Um triângulo retângulo de hipotenusa gira em torno de um dos seus catetos gerando um cone circular reto. Determine o raio, a altura e o volume do cone de mairo volume que pode ser gerado dessa maneira.
Passo 1
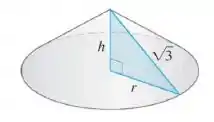
O volume vai ser:
Por Pitágoras:
Como temos na fórmula do volume, vamos ter:
Assim, nosso volume fica:
Onde o valor de vai de , até . Isso porque o não pode ser negativo e ele é menos
Passo 2
Para acharmos o valor de mínimo ou máximo, temos que comparar o valor da função nos pontos críticos e nos extremos do intervalo.
Primeiro fazemos:
Derivando ,
Fazendo isso igual a
Mas não pode ser negativo, então:
Passo 3
Vamos achar o valor da função nos pontos críticos e extremos do intervalo:
Vamos ter:
O maior dos valores é quando
Então:
Além disso
Resposta
Exercícios de Livros Relacionados
Ache as dimensões do maior jardim retangular que pode ser fechado com 100 m de cerca.
Suponha que o fabricante do Exercício 1 faça as latas abertas de pedaços quadrados de flandres com k cm de lado. Determine o comprimento do quadrado a ser cortado, de tal forma que o volume da caixa s
Ache as dimensões do maior jardim retangular, de forma que uma casa limite um lado do jardim e 100 m de cerca sejam usados.
Ache as dimensões do maior campo retangular que pode ser fechado com 240 m de cerca.
Um fabricante de latas sem tampas deseja usar folhas-de-flandres com dimensões de 8 cm por 15 cm, cortando quadrados iguais dos quatro cantos e dobrando os lados para cima. Use o método dessa seção pa